雅乐网

Logistic Regression

0. Visualizing the data

读取数据的代码

data = load('ex2data1.txt');
X = data(:, [1, 2]); y = data(:, 3);

ex2data1的内容

34.62365962451697,78.0246928153624,0
30.28671076822607,43.89499752400101,0
35.84740876993872,72.90219802708364,0
60.18259938620976,86.30855209546826,1
79.0327360507101,75.3443764369103,1

第一列是exam1的分数，第二列是exam2的分数，第三列是是否被录取。

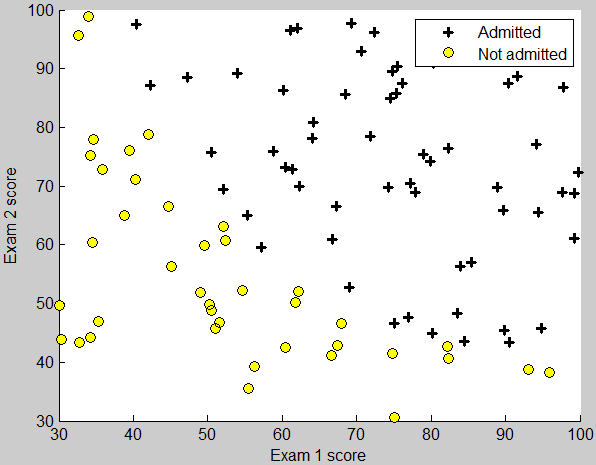
这部分要求把已有的数据用散点图的形式画出。

录取的点用+表示，未录取的点用圆圈o表示。plotData函数的框架如下

function plotData(X, y)
	figure; hold on;
	%====================== YOUR CODE HERE ======================
	hold off;
end

此时X有两列，分别是exam1和exam2的分数。对应y等于1时，用+画点；y等于0时，用o画点。下面是一种通过循环的方式

m = length(y);
for i = 1 : m
    if y(i) > 0
        plot(X(i, 1), X(i, 2), 'k+', 'LineWidth', 2, ...
            'MarkerSize', 7);
    else
        plot(X(i, 1), X(i, 2), 'ko', 'MarkerFaceColor', 'y', ...
            'MarkerSize', 7);
    end
end

plot函数中的三个点号 … 是表示换行，为了避免一行太长。

但是这样有个问题，后面的代码中

 % Specified in plot order
legend('Admitted', 'Not admitted')

图示是按照plot的顺序出现的，由于plot了多次，导致图示不正确。下面是向量化的方法

pos = find(y == 1);
neg = find(y == 0);

plot(X(pos, 1), X(pos, 2), 'k+', 'LineWidth', 2, ...
    'MarkerSize', 7);
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'y', ...
    'MarkerSize', 7);

find()返回的是所有满足条件的下标。这样就不用循环了。

运行效果如图

1. sigmoid function

要求实现函数

$$g(z) = \frac{1}{1 + e^{-z}}$$

实现时z可能是向量，要对每个元素都做计算

function g = sigmoid(z)
    g = zeros(size(z));
    g = 1 ./ (1 + exp(-z));
end

 2. Cost function and gradient

先来看一下计算前的准备工作

 %% ============ Part 2: Compute Cost and Gradient ============
 %  In this part of the exercise, you will implement the cost and gradient
 %  for logistic regression. You neeed to complete the code in 
 %  costFunction.m

 %  Setup the data matrix appropriately, and add ones for the intercept term
[m, n] = size(X);

 % Add intercept term to x and X_test
X = [ones(m, 1) X];

 % Initialize fitting parameters
initial_theta = zeros(n + 1, 1);

 % Compute and display initial cost and gradient
[cost, grad] = costFunction(initial_theta, X, y);

X是个矩阵，它每列表示一个特征，每行表示一个实例。theta是n+1个元素的列向量。y是m个元素的结果向量。

代价函数公式

$$J(\theta) = – \frac{1}{m} \sum_{i = 1}^{m} \left( y^{(i)} log(h(x^{(i)})) + (1-y^{(i)}) log\left(1-h(x^{(i)})\right) \right)$$

可以先用一个变量hx求出h(x)，利用1中的函数

$$ h(x) = \frac{1}{1 + e^{- \theta^T x}} $$$

hx = sigmoid(X * theta);

求和号中每一项对应一行，可以使用向量化的方法计算，最后用sum求和。

J = (-1/m) * sum(y .* log(hx) + (1-y) .* log(1 - hx));

梯度的计算公式

$$\frac{\partial}{\partial \theta_j} J(\theta) = \frac{1}{m} \sum_{i=1}^{m}\left( \left(h(x^{(i)}) – y^{(i)}\right) x_j^{(i)} \right)$$

最终的代码

function [J, grad] = costFunction(theta, X, y)
    m = length(y); % number of training examples
    grad = zeros(size(theta));

    hx = sigmoid(X * theta);
    J = (-1/m) * sum(y .* log(hx) + (1-y) .* log(1 - hx));

    n = length(theta);
    for j = 1 : n
        grad(j) = sum((hx - y) .* X(:, j)) / m;
    end
end

3. fminunc

关键代码如下

 %  Set options for fminunc
options = optimset('GradObj', 'on', 'MaxIter', 400);
 %  Run fminunc to obtain the optimal theta
 %  This function will return theta and the cost 
[theta, cost] = ...
	fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);
 % Plot Boundary
plotDecisionBoundary(theta, X, y);

fminunc中的@(t)(costFunction(t, X, y))是为了把函数costFunction转换为只接受一个参数t的函数。

调用plotDecisionBoundary函数画出点和决策边界，其中相关的代码如下（两个参数的情况）

if size(X, 2) <= 3
    % Only need 2 points to define a line, so choose two endpoints
    plot_x = [min(X(:,2))-2,  max(X(:,2))+2];

    % Calculate the decision boundary line
    plot_y = (-1./theta(3)).*(theta(2).*plot_x + theta(1));

    % Plot, and adjust axes for better viewing
    plot(plot_x, plot_y)
    
    % Legend, specific for the exercise
    legend('Admitted', 'Not admitted', 'Decision Boundary')
    axis([30, 100, 30, 100])

ex2的第104行是不需要的，因为在上面函数里已经添加了图示。在运行legend(‘Admitted’, ‘Not admitted’)反而会覆盖掉分界线的图示。

4. predict

通过3得出了参数，现在就可以预测了。我们有结论

\(\theta^T x > 0\)时，对应h(x) > 0.5，应该预测结果为1；

\(\theta^T x < 0\)时，对应h(x) < 0.5，应该预测结果为0；

因此代码为

function p = predict(theta, X)
    p = ((X * theta) >= 0);
end

Regularization

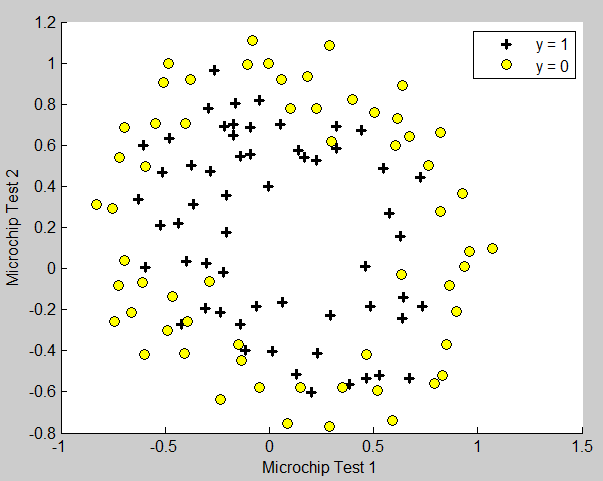
1. Visualizing the data

这部分使用的代码和上面的相同

但这次的数据不能用直线来拟合出边界。

2. Feature mapping

使用已有的特征的幂来当做新的特征，这里最高6次幂。代码如下

function out = mapFeature(X1, X2)
 % MAPFEATURE Feature mapping function to polynomial features
 %
 %   MAPFEATURE(X1, X2) maps the two input features
 %   to quadratic features used in the regularization exercise.
 %
 %   Returns a new feature array with more features, comprising of 
 %   X1, X2, X1.^2, X2.^2, X1*X2, X1*X2.^2, etc..
 %
 %   Inputs X1, X2 must be the same size
 %
degree = 6;
out = ones(size(X1(:,1)));
for i = 1:degree
    for j = 0:i
        out(:, end+1) = (X1.^(i-j)).*(X2.^j);
    end
end

end

 3. Cost function and gradient

公式如下

$$J(\theta) = – \left[ \frac{1}{m} \sum_{i = 1}^{m} \left( y^{(i)} log(h(x^{(i)})) + (1-y^{(i)}) log\left(1-h(x^{(i)})\right) \right) \right] + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2$$

theta_0和之前的相同，其余的参数在最后加了\(\frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2\)

代码如下

    hx = sigmoid(X * theta);
    J = (-1/m) * sum(y .* log(hx) + (1-y) .* log(1 - hx)) + ...
        (lambda/(2*m)) * (sum(theta .* theta) - theta(1)^2);

要注意减掉theta(1)的平方，因为公式中不包含 \(\theta_0\)，所以需要去掉。

梯度下降的算法公式

$$\frac{\partial}{\partial \theta_0} J(\theta) = \frac{1}{m} \sum_{i=1}^{m} \left(h(x^{(i)}) – y^{(i)}\right) x_0^{(i)} $$

$$\frac{\partial}{\partial \theta_j} J(\theta) = \left( \frac{1}{m} \sum_{i=1}^{m} \left(h(x^{(i)}) – y^{(i)}\right) x_j^{(i)} \right) + \frac{\lambda}{m}\theta_j$$

计算代码

function [J, grad] = costFunctionReg(theta, X, y, lambda)
	m = length(y); % number of training examples
	grad = zeros(size(theta));

    hx = sigmoid(X * theta);
    J = (-1/m) * sum(y .* log(hx) + (1-y) .* log(1 - hx)) + ...
        (lambda/(2*m)) * (sum(theta .* theta) - theta(1)^2);

    grad(1) = (1/m) * sum((hx - y) .* X(:, 1));
    n = length(theta);
    for j = 2 : n
        grad(j) = (1/m) * sum((hx - y) .* X(:, j)) + (lambda / m) * theta(j);
    end
end

4. plotDecisionBoundary

画出非线性边界的代码

else
    % Here is the grid range
    u = linspace(-1, 1.5, 50);
    v = linspace(-1, 1.5, 50);

    z = zeros(length(u), length(v));
    % Evaluate z = theta*x over the grid
    for i = 1:length(u)
        for j = 1:length(v)
            z(i,j) = mapFeature(u(i), v(j))*theta;
        end
    end
    z = z'; % important to transpose z before calling contour

    % Plot z = 0
    % Notice you need to specify the range [0, 0]
    contour(u, v, z, [0, 0], 'LineWidth', 2)
end

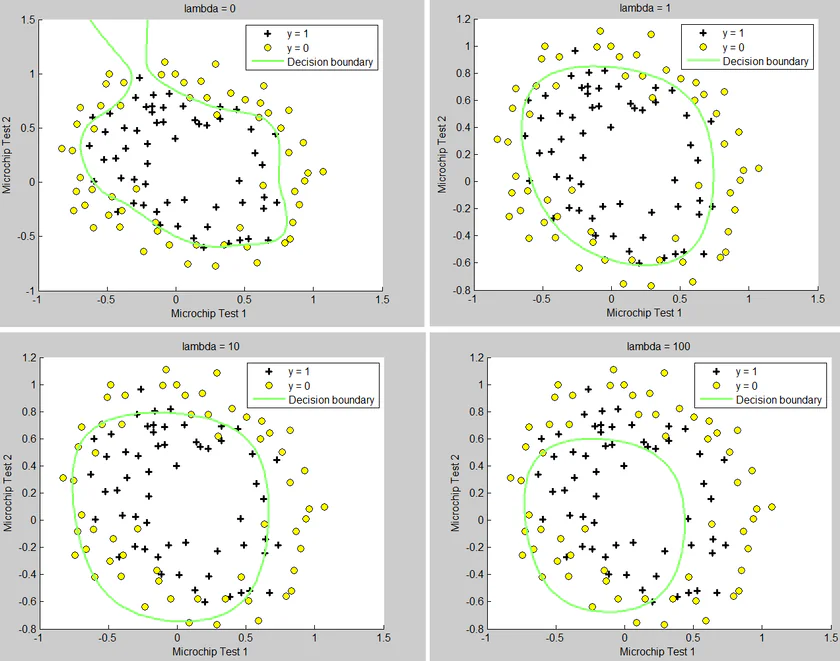
5. change regularization parameters

修改ex2_reg.m第90行可以修改lambda的大小，等于0对应不进行正则化。