红黑树各种操作思路见 从B-树角度理解红黑树背后的原理 ，本文是红黑树的C++实现。但并没有全面的测试，如果大家发现了bug，欢迎指出。
本文的红黑树是从前面的BST继承而来，也是用到了AVL中用到的3+4重构和旋转操作。编译时要用到前面的BST.h Bintree.h 以及vector、stack、queue这些数据结构。
所有源代码地址：yalewoo/cpp-data-structure · GitHub
RBTree.h
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 |
#ifndef RBTREE_H #define RBTREE_H #include "BST.h" #define IsBlack(x) ( (x) == 0 || (x)->color == BLACK ) #define IsRed(x) ( !IsBlack(x) ) template <typename T> class RBT : public BST<T>{ public: RBT(); virtual BinNodePosi(T) insert(const T &); virtual bool remove(const T &); protected: using BST<T>::_root; using BST<T>::_size; using BST<T>::_hot; using BST<T>::search; using BST<T>::siblingOf; using BST<T>::connect34; using BST<T>::removeAt; void solveDoubleRed(BinNodePosi(T) x); void solveDoubleBlack(BinNodePosi(T) r); void rotateLL(BinNodePosi(T) t1, BinNodePosi(T) t2); void rotateRR(BinNodePosi(T) t2, BinNodePosi(T) t1); virtual int updateHeight(BinNodePosi(T) x); }; //更新某结点的黑高度 template <typename T> int RBT<T>::updateHeight(BinNodePosi(T) x) { if (!x) return -1; x->height = max(stature(x->lchild), stature(x->rchild)); if (x->color == BLACK) ++x->height; return x->height; } template <typename T> RBT<T>::RBT() { _hot = 0; _size = 0; } template <typename T> BinNodePosi(T) RBT<T>::insert(const T & e) { BinNodePosi(T) p = search(e); if (p != NULL && p->data == e) //already exist { return p; } BinNodePosi(T) x = BST<T>::insert(e); p = x->parent; //新插入结点是根节点时 if (p == 0) { x->color = BLACK; x->height = 1; return x; } x->color = RED; //若p结点是黑色 红黑树的性质没有破坏 if (p->color == BLACK) { return x; } //若p是红色 出现双红缺陷 solveDoubleRed(x); //++_size; return x; } template <typename T> void RBT<T>::solveDoubleRed(BinNodePosi(T) x) { BinNodePosi(T) p = x->parent; BinNodePosi(T) g = p->parent; BinNodePosi(T) u = siblingOf(p); if (IsBlack(u)) //情况2.1 p红u黑 { BinNodePosi(T) par = g->parent; enum {ROOT, LEFT, RIGHT} ptoc; if (g->parent) { if (g == g->parent->lchild) ptoc = LEFT; else ptoc = RIGHT; } else ptoc = ROOT; BinNodePosi(T) t1; BinNodePosi(T) t2; BinNodePosi(T) t3; BinNodePosi(T) st1; BinNodePosi(T) st2; BinNodePosi(T) st3; BinNodePosi(T) st4; if (g->lchild && x == g->lchild->lchild) { t1 = x; t2 = p; t3 = g; st1 = x->lchild; st2 = x->rchild; st3 = p->rchild; st4 = g->rchild; } else if (g->lchild && x == g->lchild->rchild) { t1 = p; t2 = x; t3 = g; st1 = p->lchild; st2 = x->lchild; st3 = x->rchild; st4 = g->rchild; } else if (g->rchild && x == g->rchild->lchild) { t1 = g; t2 = x; t3 = p; st1 = g->lchild; st2 = x->lchild; st3 = x->rchild; st4 = p->rchild; } else { t1 = g; t2 = p; t3 = x; st1 = g->lchild; st2 = p->lchild; st3 = x->lchild; st4 = x->rchild; } t2->parent = par; switch (ptoc) { case ROOT : _root = t2; break; case LEFT : par->lchild = t2; break; case RIGHT : par->rchild = t2; break; } connect34(t1, t2, t3, st1, st2, st3, st4); t2->color = BLACK; t1->color = RED; t3->color = RED; t2->height++; t3->height--; } else //情况2.2 p红u红 { p->color = BLACK; u->color = BLACK; g->color = RED; p->height++; g->height--; if (g->parent == 0) g->color = BLACK; else if (IsRed(g->parent)) solveDoubleRed(g); } } template <typename T> bool RBT<T>::remove(const T & e) { //如果已存在则返回false BinNodePosi(T) x = search(e); if (!x) return false; //左右孩子都存在时，与中序后继交换元素 保证删除时有一个孩子为空 if (x->lchild && x->rchild) { BinNodePosi(T) p = x->succ(); T tmp = x->data; x->data = p->data; p->data = tmp; x = p; } BinNodePosi(T) r = removeAt(x); //如果删除后变为空树 直接返回 if ((_size) == 0) return true; //如果删除的是根节点重新将根节点染黑 并更新高度 if (_hot == 0) { _root->color = BLACK; updateHeight(_root); return true; } //x和r有一个为红 if (IsRed(x) || IsRed(r)) { if (IsRed(r)) r->color = BLACK; return true; } else { solveDoubleBlack(r); } delete x; return true; } template <typename T> void RBT<T>::solveDoubleBlack(BinNodePosi(T) r) { BinNodePosi(T) p = r ? r->parent : _hot; if (p == 0) return; BinNodePosi(T) s = ( r == p->lchild ? p->rchild : p->lchild ); if (IsBlack(s)) { if ( IsRed(s->lchild) || IsRed(s->rchild) ) //情况1 s为黑 t为红 { BinNodePosi(T) t; if (IsRed(s->rchild)) t = s->rchild; if (IsRed(s->lchild)) t = s->lchild; BinNodePosi(T) g = p; BinNodePosi(T) p1 = s; BinNodePosi(T) x = t; BinNodePosi(T) par = g->parent; enum {ROOT, LEFT, RIGHT} ptoc; if (g->parent) { if (g == g->parent->lchild) ptoc = LEFT; else ptoc = RIGHT; } else ptoc = ROOT; BinNodePosi(T) t1; BinNodePosi(T) t2; BinNodePosi(T) t3; BinNodePosi(T) st1; BinNodePosi(T) st2; BinNodePosi(T) st3; BinNodePosi(T) st4; if (g->lchild && x == g->lchild->lchild) { t1 = x; t2 = p1; t3 = g; st1 = x->lchild; st2 = x->rchild; st3 = p1->rchild; st4 = g->rchild; } else if (g->lchild && x == g->lchild->rchild) { t1 = p1; t2 = x; t3 = g; st1 = p1->lchild; st2 = x->lchild; st3 = x->rchild; st4 = g->rchild; } else if (g->rchild && x == g->rchild->lchild) { t1 = g; t2 = x; t3 = p1; st1 = g->lchild; st2 = x->lchild; st3 = x->rchild; st4 = p1->rchild; } else { t1 = g; t2 = p1; t3 = x; st1 = g->lchild; st2 = p1->lchild; st3 = x->lchild; st4 = x->rchild; } t2->parent = par; switch (ptoc) { case ROOT : _root = t2; break; case LEFT : par->lchild = t2; break; case RIGHT : par->rchild = t2; break; } connect34(t1, t2, t3, st1, st2, st3, st4); t2->color = g->color; t1->color = BLACK; t3->color = BLACK; } else //情况2 s为黑 s的两个孩子为黑 { s->color = RED; --s->height; if (IsRed(p)) //情况2.1 s为黑 s的两个孩子均为黑 p为红 { p->color = BLACK; } else //s为黑 s的两个孩子均为黑 p为黑 { p->height--; solveDoubleBlack(p); } } } else //情况3 s为红 { if (s == p->lchild) { rotateLL(s, p); } else { rotateRR(s, p); } s->color = BLACK; p->color = RED; solveDoubleBlack(r); } } template <typename T> void RBT<T>::rotateLL(BinNodePosi(T) t1, BinNodePosi(T) t2) { //t2 --> st2 t2->lchild = t1->rchild; //st2 --> t1 if (t1->rchild) t1->rchild->parent = t2; //t1 --> t2 t1->rchild = t2; //父节点 --> t1（树根情况） if (t2->parent == NULL) { t1->parent = NULL; this->_root = t1; t2->parent = t1; return; } //t1 --> 父节点 t1->parent = t2->parent; //父节点 --> t1（非树根） if (t2->parent->lchild == t2) t2->parent->lchild = t1; else t2->parent->rchild = t1; //t2 --> t1 t2->parent = t1; } template <typename T> void RBT<T>::rotateRR(BinNodePosi(T) t2, BinNodePosi(T) t1) { //t1 --> st2 t1->rchild = t2->lchild; //st2 --> t1 if (t2->lchild) t2->lchild->parent = t1; //t2 --> t1 t2->lchild = t1; //父节点 --> t2（树根） if (t1->parent == NULL) { this->_root = t2; t2->parent = NULL; t1->parent = t2; return; } //t2 --> 父节点 t2->parent = t1->parent; //父节点 --> t2（非树根） if (t1->parent->lchild == t1) t1->parent->lchild = t2; else t1->parent->rchild = t2; //t1 --> t2 t1->parent = t2; } #endif |
RBTree.cpp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
#include <iostream> #include "RBTree.h" int main() { RBT<int> rb; rb.insert(12); rb.display(); rb.insert(1); rb.display(); rb.insert(9); rb.display(); rb.insert(2); rb.display(); rb.insert(0); rb.display(); rb.insert(11); rb.display(); rb.insert(7); rb.display(); rb.insert(5); rb.display(); rb.insert(4); rb.display(); rb.display(); rb.remove(12); rb.display(); rb.remove(1); rb.display(); rb.remove(9); rb.display(); rb.remove(2); rb.display(); rb.remove(0); rb.display(); rb.remove(11); rb.display(); rb.remove(7); rb.display(); rb.remove(5); rb.display(); rb.remove(4); rb.display(); rb.display(); return 0; } |
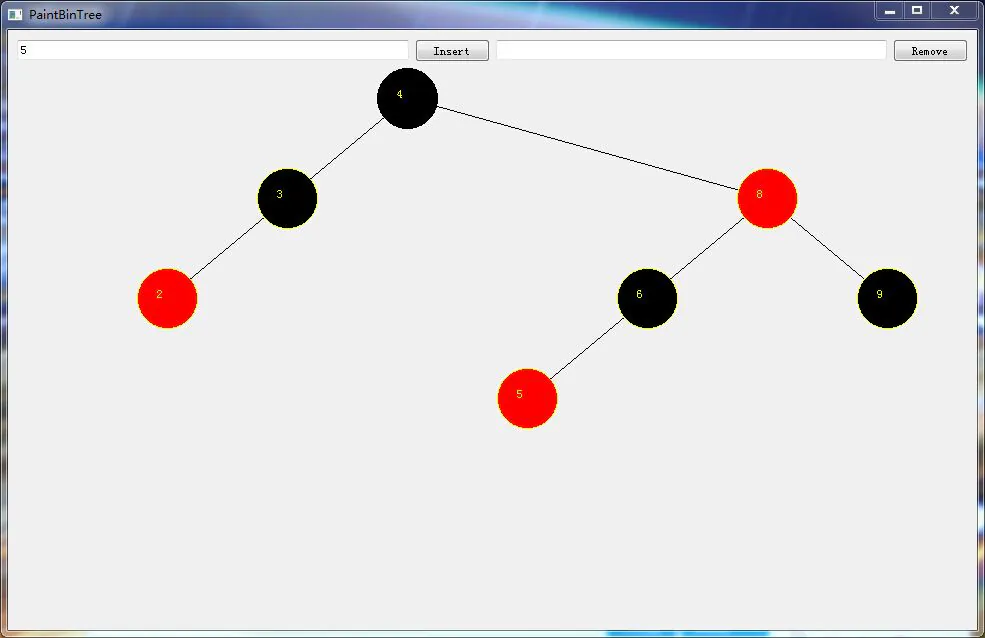
使用QT显示红黑树
和二叉树的显示代码基本一致，不同的只是把画板中的BST改成RBT，画的时候根据结点颜色来修改画刷颜色。
运行效果
支付宝打赏 
微信打赏