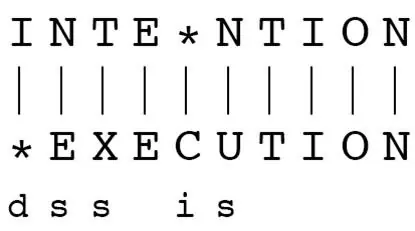
Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)
You have the following 3 operations permitted on a word:
a) Insert a character
b) Delete a character
c) Replace a character
思路
d[i][j]表示word1的前i个字符到word2的前j个字符的距离
一、word1[i] == word2[j] 时， d[i][j] = d[i-1][j-1]
二、word1[i] != word2[j] 时，取下面三种情况的最小者
1. d[i-1][j] + 1 （添加）
2. d[i][j-1] + 1 （删除）
3. d[i-1][j-1] + 1 （替换）
初始条件：
d[i][0] = i
d[0][j] = j
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
int minDistance(string word1, string word2) { int len1 = word1.size(); int len2 = word2.size(); vector<vector<int> > d(len1+1, vector<int>(len2+1, 0)); for (int i = 0; i <= len1; ++i) { d[i][0] = i; } for (int j = 0; j <= len2; ++j) { d[0][j] = j; } for (int i = 1; i <= len1; ++i) { for (int j = 1; j <= len2; ++j) { if (word1[i-1] == word2[j-1]) d[i][j] = d[i-1][j-1]; else { d[i][j] = min(min(d[i-1][j]+1, d[i][j-1] + 1), d[i-1][j-1]+1); } } } return d[len1][len2]; } |
支付宝打赏 
微信打赏