本文是 TsinghuaX: 60240013X 组合数学(2015春)第二周的笔记1。
计数,也就是计算所有符合要求的情况的数量。它的关键是要无重复、无遗漏的包含所有的情形。这不仅出现在我们生活中的一些问题中,而且对于编写程序、分析算法复杂度也有很大的帮助。本文介绍常用的排列组合公式,以及应用的举例。
加法法则和乘法法则
加法法则和乘法法则应该是最简单最朴素的法则了,也是计数的基本法则。但要注意应用这两个法则的必要条件是A问题和B问题是独立的。
加法法则适用于分类,而乘法法则适用于分步。
若A问题有a种方案,B问题有b种方案,那么A或B,也就是A选1种或B选一种,适用加法法则,共a+b种方案。
问题1:某班级男生25人,女生5人,共有25+5=30人
如果问题是A与B,即A选1种方案,且B选一种方案,共有a*b种方案。
问题2:男生25人,女生5人,从男生中选1人,女生中选1人,共有25*5=125种
分类的思想
问题3:男生25人,女生5人,从男生中选1人,从女生中选1人,但要求男生A和女生B不能同时选,共有多少种方案呢?
可以把方案分成两类:选男生A和不选男生A。
选男生A时:只需要从不是B的女生中选1人,共5-1=4种
不选男生A:男生剩下24种,女生5种,共24*5=120种。
一共有4+120=124种
减法法则
减法法则就是求出全集的种类数,再减掉需要求解问题的反面情况数。
问题3就是应用减法法则的一个例子。男生A和女生B不能同时选的反面是同时选AB,只有1种情况。那么问题答案是总问题数减去1 也就是125-1=124
除法法则
问题4:男生有25人,分成5组,每组25/5=5人
无重排列和无重组合
高中课本里的排列组合实际上就是无重排列和无重组合。相信大家都很熟悉,下面简单的回顾一下它们的定义:
从n个不同的元素中,取r个不重复的元素,按次序排列,称为从n个中取r个的无重排列。记作P(n, r)
从n个不同元素中取r个不重复的元素组成一个子集,而不考虑其元素的顺序,称为从n个中取r个的无重组合。记作C(n, r)
排列组合的公式是通过建立问题的模型应用上面的加法乘法等法则写出来的,下面先贴出结果:
排列的放球模型
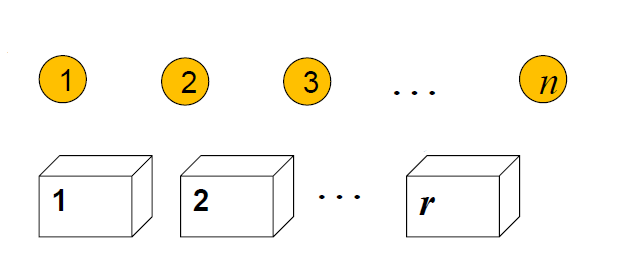
排列问题可以看做这个问题:从n个不同的球中,取出r个放入r个不同的盒子里,每盒1个。共有多少种方法?
这个问题可以根据盒子来进行计数:第1个盒子可以选n种球,共n种,第2个盒子可以选第一个盒子里的球之外的n-1种球,第3个盒子可以选第1、2个盒子里的球之外的n-2种球,……,第r个盒子可以选前面r-1个盒子之外的n-(r-1) = n-r+1 种球。
应用乘法法则,总的方案数: n * (n-1) * (n-2) * …… * (n-r+1) 。分子分母同时乘以n-r的阶乘就得到了上面的公式。
排列的两个恒等式
同一个问题从不同的角度或不同的步骤,我们可以通过不同的计算方法计算出同一个结果。
排列的恒等式1:P(n, r) = n * P(n-1, r-1)
从n个中选出r个,这个恒等式使用了分步的思想:
第一步,从n个中取出1个,共n种取法
第二步,从剩下的n-1个中,取出r-1个。
排列的恒等式2:P(n, r) = P(n-1, r) + r * P(n-1, r-1)
使用分类的思想:分为两种情况:不选择1号球和选择1号球。
不选择1号球:方案是从剩下的n-1个中选择r个,P(n-1, r)
选择1号球:第1步,1号球放入r个盒子,共r种;第2步,剩下的n-1个球放入r-1个盒子,共P(n-1, r-1)种。总共 r * P(n-1, r-1)
组合的放球模型
组合中不考虑元素的顺序,因此对应放球模型中的盒子没有区别。排列中盒子的组合共有r!种,应用除法法则就可以得到组合和排列的关系:
组合数等于排列数 除以 盒子的排列数
组合的格路模型
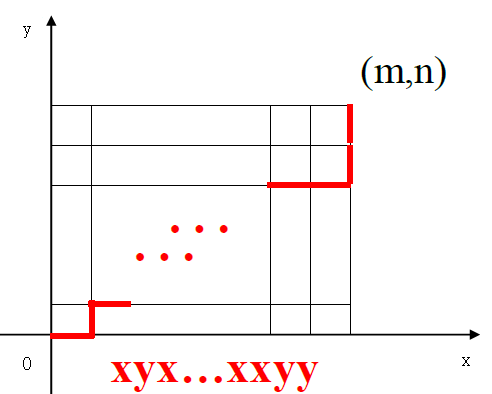
从 (0,0)点出发沿x轴或y轴的正方向每步走一个单位,最终走到(m,n)点,其路径数是C(m+n,n)
从(0,0)走到(m,n),一共要走m+n步,每步可以沿x方向或y方向。共可以沿x方向走m步,沿y方向走n步。
总的方案数就是从m+n步中,选出n个沿y方向的步。
组合的恒等式
C(n, r) = C(n, n-r)
从n个球选r个,剩余n-r个。显然r个有多少种选法,剩余的n-r个就有多少种方案。
C(n, l) * C(l, r) = C(n, r) * C(n-r, l-r)
左边:一个班级有n个同学,选出l个班委,再从班委中选出r个班长。
右边:先从n个同学中选出r个班长。再从剩下的n-r个同学中选出l-r个班委。
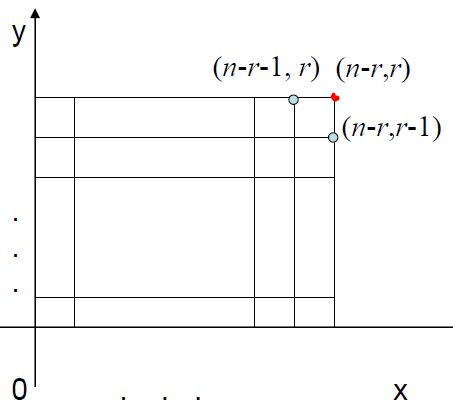
C(n, r) = C(n-1, r) + C(n-1, r-1)
可以使用格路模型来分析,C(n, r)对应走到(n-r , r) 有两类情况:
还可以使用分类的思想:n个里面取r个分成两种情况:
不取1号球:从剩下的n-1个球中取r个,共C(n-1, r)种
取1号球:从剩下的n-1个中取r-1个,共C(n-1, r-1)种
C(m+n, r)=C(m,0)C(n, r)+C(m, 1)C(n,r-1)+ …+C(m, r)C(n, 0)
这个可以看做根据m中取得个数进行分类:m中取0个、1个……r个。加起来即可。
组合和二项式定理
这个可以看做n个(a+b),每个可以选a或者选b,例如 (a+b)^7 展开后,a^3b^4的系数就是7个里面选3个a C(7, 3)
特别的,a=b=1时有公式
a=1,b=-1时有公式:
例:(2a + b + c) ^ 6展开式中,a^2 b^2 c^2的系数
从6个(2a+b+c)中,选出2个2a ,共C(6, 2)种,选出2个b,共C(4,2)种。
2a的平方系数还有2^2 = 4
因此答案是4 * C(6, 2) * C ( 4, 2) = 360
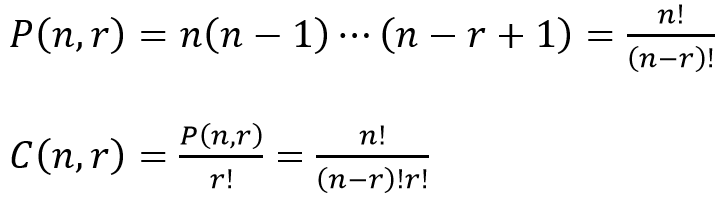
 支付宝打赏
支付宝打赏  微信打赏
微信打赏