本文是 TsinghuaX: 60240013X 组合数学(2015春)第二周的笔记2。
更多的排列
圆排列
圆排列就是围成一个圆。圆旋转一下是同一个排列。因此
从n个中取r个的圆排列的排列数为 P(n,r)/r
这是因为r个中间有r个空隙,沿着r个空隙剪开可以分别得到r中排列。
项链排列
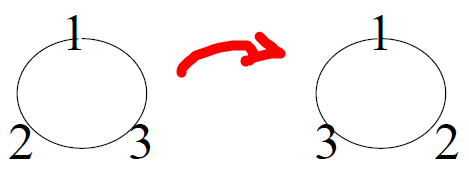
项链排列和圆排列不同的地方是项链是立体的,可以翻过来,是同一种排列
因此,项链排列的公式是P(n, r)/2r
可重排列
可重排列是指,每一种可以选择多次。例如
26个英文字母可以组成多少个4位数的字符串?答案是26^4种。
26个英文字母可以组成多少个4位数的字符串,其中每位都不相同?这相当于26个选4个的排列。答案是P(26, 4)
多重排列
多重排列中,某一种可以出现多次,但是是有限的次数。例如:
pingpang这8个字符有多少种排列?
2个p, 2个n,2个g,1个i,1个a。我们可以首先把两个的看出不同的,然后除以重复的次数
8个字符的排列P(8, 8) 除以重复的次数 2*2*2 = 8! / 2*2*2
可重组合
从A={1,2,3….n}中取r个元素{a1,a2,…ar},ai∈A,i=1,2,..r,且允许ai=aj, i≠j
可重组合的放球模型:取r个无区别的球,n个有区别的盒子,每个盒子允许放0个1个或多个球。
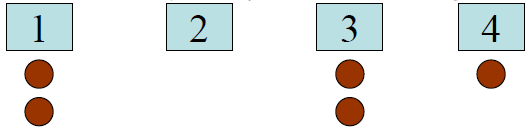
对应的实际问题:有梨(1号水果)、苹果(2号水果)、橘子(3号水果)、香蕉(4号水果)4种水果,从中选出5个。
这相当于5个无区别的球,4个有区别的盒子。
这种方案对应2个梨(1号水果),2个橘子(3号水果),1个香蕉(4号水果)。
一一对应的方法
我们可以按照盒子的序号1-n ,盒子里有几个球,这个序号就写几次,那么上面的方案就可以表示为
1 1 3 3 4
共有5个数字,我们把它分别加上序号 0 1 2 3 4 就成了
1 2 5 6 8
最后的这个序列,我们可以看到 第一个数字最小是1,最后一个数字最大是5+4=9
每一种方案都可以一一对应一个1-9中选出5个数字的无重组合。
我们再来看一下普遍的情况:
r个无区别的球,n个有区别的盒子
按照盒子编号1-n,有几个球写几次 可以写出一个r个数字的序列。分别加上0 1 2 …… r-1
结果第一个数字最小是1+0 最大是n+r-1 ,无重组合的个数就是从1到n+r-1中选出r个不重复的数字。
因此,无重组合的公式为:r个无区别的球,n个有区别的盒子 共有 C(n+r-1,r) 种。
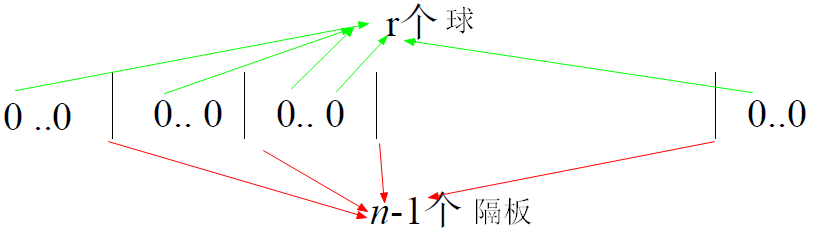
隔板法
可以转化为 r个球,插入n-1个隔板。一共有r+n-1个位置,从中选出r个位置放球。得到结果C(n+r-1,r)
线性方程的非负整数解
线性方程x1+x2…+xn=b的非负整数解的个数是C(n+b-1,b)
这相当于b个无区别的球,n个有区别的盒子(x1到xn)
不相邻组合
不相邻的组合是指从A={1,2,…n}中取r个不相邻的数进行组合(不可重),即不存在相邻的两个数j, j+1的组合
从A={1,2,…n}中取r个不相邻的数进行组合,其组合数为C(n-r+1,r)
可以采用和无重组合类似的一一对应的方法:不同的是这里减去序号0 1 2 3……因为不相邻,所以减去后也是不可能相同的。
因此这也可以转化为1 到 n-r+1 种选r个的无重组合。
例
某保密装置须同时使用若干把不同的钥匙才能打开。现有7人,每人持若干钥匙。须4人到场,所备钥匙才能开锁。
1.至少有多少把不同的锁?
2.每人至少持几把钥匙?
解
1. 每3人至少缺1把钥匙,任意4个人都不缺钥匙,则要求每3人所缺钥匙不同。
–如果abc缺的钥匙和abd缺的钥匙一样,那abcd就不能开门
•故至少共有C(7,3)=35把不同的锁。
2.任意4个人都不缺钥匙,任一人对于其他6人中的每3人,都至少有1把钥匙与之相配才能开锁。故每人至少持C(6,3)=20把不同的钥匙。
全排列
把所有的排列列举出来就可以生成全排列。全排列的生成算法就是对于给定的字符集,用有效的方法将所有可能的全排列无重复无遗漏地枚举出来。
字典序法生成全排列
按照字典中的顺序。可以参考英文字典。
字典中,每个排列有唯一的前驱和后继,相邻排列之间差尽可能的小。
算法实现
SJT全排列生成算法
1) 找到最大的可移动数m(当一个数指向一个比它小的数是,该数就是可移动数)
2) 交换m和m所指向的数
3) 改变所有比m大的数的方向
4) 重复上面的步骤,直至找不到可移动数
库函数中的全排列生成函数
C++标准程序库中有两个函数next_permutation, prev_permutation,可以生成字典序排列。
Stirling公式
全排列的个数可能超出我们的想象。10个字符的全排列有10! = 3628800种。20个字符的全排列有2432902008000000000种。
Stirling公式可以用来估计n!的大小。n越大,估计越精确。
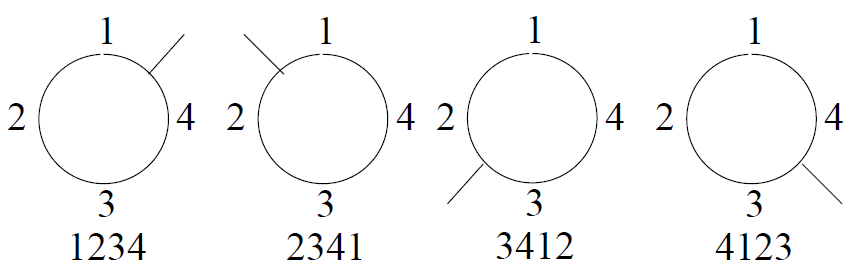
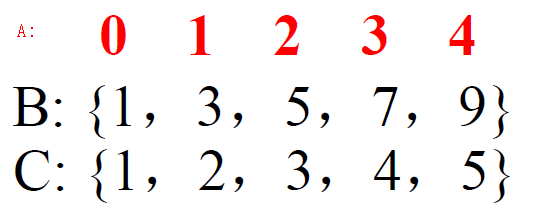


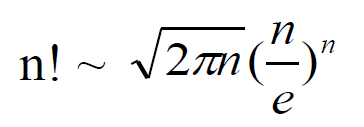
 支付宝打赏
支付宝打赏  微信打赏
微信打赏