雅乐网

队列是一种常用的数据结构。如果按照常规的想法，要获得队列中的最大值，必须遍历队列中的所有元素，时间复杂度为O(n)。怎么降低这个时间呢？求最大元素很容易想到堆。如果建立一个辅助的最大堆（里面存放队列中元素的指针以及值），入队或者出队的时候，对辅助最大堆进行调整。这种方法入队和出队时间复杂度为O(logn)，获取最大值复杂度为O(1)。有没有更好的办法呢？

使用两个栈模拟队列

这个办法是基于两个事实的：用两个栈可以模拟一个队列；栈可以通过辅助栈实现O(1)的取最大值操作。

下面的代码示例为了简洁和突出本质，栈内的元素为int类型，并且没有进行合法检查。

栈的实现

栈是后进先出的数据结构，由于push和pop都是在栈顶，可以使用数组来模拟，每次操作都在数组的尾部，这样时间复杂度为O（1）.

class Stack
{
	int _top;
	int *elem;
public:
	Stack(int n) : _top(0)
	{
		elem = new int[n+1];
		elem[0] = -1;
	}
	void push(int n)
	{
		elem[++_top] = n;
	}
	int pop()
	{
		return elem[_top--];
	}
	int top()
	{
		return elem[_top];
	}
	bool empty() { return !_top; }
	~Stack()
	{
		if (elem) delete[] elem;
	}
};

上面这段代码实现了简单的 入栈push(int n)，出栈pop()和栈顶元素 top()操作。

获取Stack中的最大值

设置一个记录当前最大值的辅助栈nowmax，保存当前栈内元素的最大值。

入栈的时候，如果比nowmax栈顶元素大，就nowmax.push进去

如果入栈元素比nowmax栈顶元素小，则入栈元素对栈内最大值没有影响，nowmax栈不进行操作。

出栈的时候，如果出栈元素等于nowmax的栈顶，就进行nowmax的pop操作。

如果出栈元素小于栈顶，则出栈的元素对栈的最大元素没有影响，nowmax不进行操作。

这样，nowmax的栈顶始终记录当前站内元素的最大值。

class StackMax
{
	Stack stk;
	Stack stkmax;
public:
	StackMax(int n) : stk(n), stkmax(n)
	{
		
	}
	void push(int n)
	{
		stk.push(n);
		if (n >= stkmax.top())
			stkmax.push(n);
	}
	int pop()
	{
		int tmp = stk.pop();
		if (tmp == stkmax.top())
			stkmax.pop();
		return tmp;
	}
	int nowmax()
	{
		return stkmax.top();
	}
	bool empty()
	{
		return stk.empty();
	}
	~StackMax()
	{
		
	}
};

 两个栈模拟一个队列

栈是后进先出的数据结构，如果经过一次pop和push，就可以变为先进先出。

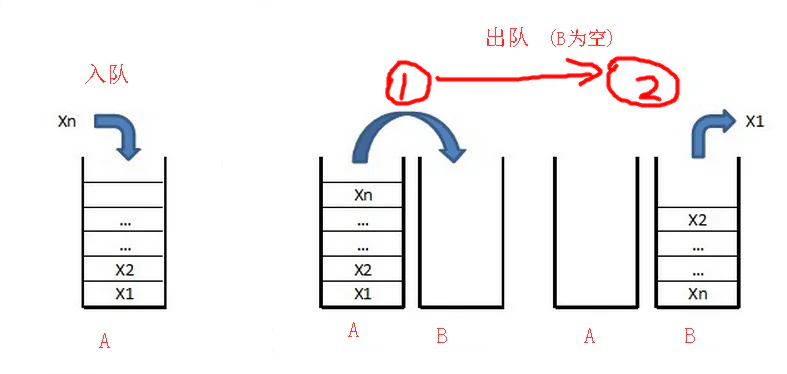
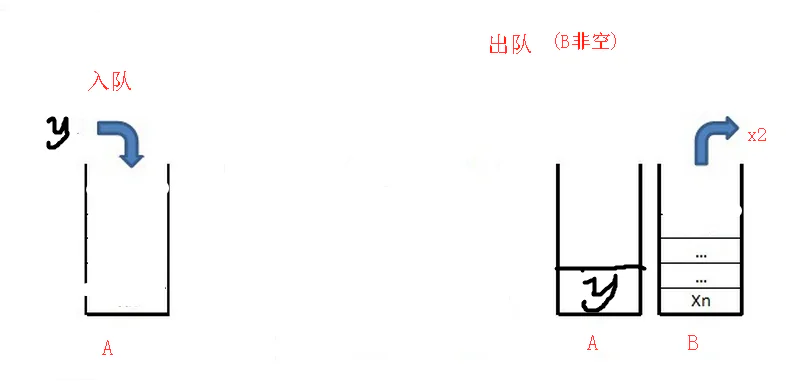
比如我们有A和B两个栈，入队的时候直接A.push()中，出队的时候，直接B.pop()。

如果B为空，那么我们需要把A中先进来的元素挪到B的栈顶位置，正好就可以依次的 B.push(A.pop()) ，完成后直接B.pop()就是最先进来的元素了。

这样就通过两个栈实现了先进先出。

获取队列的最大元素

只需要获得两个栈的最大元素，比较就可以了。

class QueueMax
{
	StackMax en;
	StackMax de;
public:
	QueueMax(int n) : en(n), de(n) { }
	void enqueue(int n)
	{
		en.push(n);
	}
	int dequeue()
	{
		if (de.empty())
		{
			while (!en.empty())
			{
				int tmp = en.pop();
				de.push(tmp);
			}
		}

		return de.pop();
	}
	int nowmax()
	{
		return en.nowmax() > de.nowmax() ? en.nowmax() : de.nowmax();
	}
	~QueueMax() {}
};

 复杂度分析

入队的时候直接执行一个栈的push，复杂度为O(1)

出队的时候，若B栈为空，需要把栈A中的所有元素pop然后push到B中，在最坏情况下需要时间复杂度O(n).但要注意的是，一旦花费O(n)的时间把A中的所有元素移动到B中后，接下来的n-1次出队只需B.pop.所需时间均为O(1).

那么针对所有的情况，我们其实可以看出，对每一个元素入队，出队。都对应A.push() A.pop B.push B.pop()这4个O(1)的操作。因此平均而言每个元素入队和出队的时间复杂度为O(1)

获取最大值，由于Stack获取最大值时间O(1)，队列要获取两个max比较 ，时间复杂度仍为O(1).

因此，使用两个栈的方法，入队出队和获取最大值，时间复杂度均为O(1)。空间复杂度约为O(4n )。