雅乐网

Leetcode 32题

Given a string containing just the characters ‘(‘ and ‘)’, find the length of the longest valid (well-formed) parentheses substring.

For “(()”, the longest valid parentheses substring is “()”, which has length = 2.

Another example is “)()())”, where the longest valid parentheses substring is “()()”, which has length = 4.

class Solution {
public:
    int longestValidParentheses(string s) {

    }
};

方法1：动态规划

用dp[i]表示以字符s[i]结尾的最长匹配的长度。

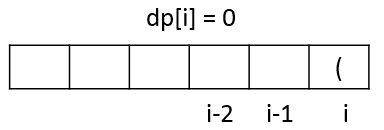
当s[i]等于'(‘时，以 ‘(‘ 结尾的字串必定不是有效的括号匹配，因此此时 dp[i]=0.

s[i]等于’)’时，要看s[i-1]。

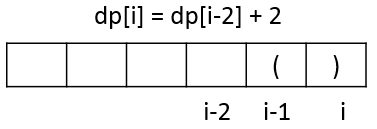
如果s[i-1]是'(‘，正好和s[i]匹配，这时，dp[i]的值就等于dp[i-2]+2

如果s[i-1]是’)’ ，这时要看以i-1结束的字串的前一个字符和s[i]是不是匹配：

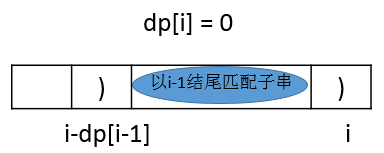
情况一：i-1结束子串的前一个字符是右括号，和s[i]不匹配，此时dp[i]=0

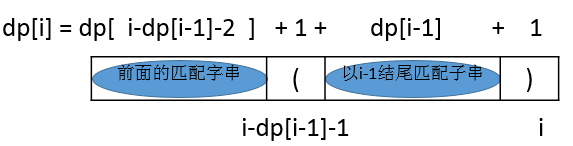
情况二：是左括号，正好匹配。

下面是代码，在s最前面加上’)’是为了上面i-2和i-dp[i-1]-2不会越界，并且不影响最后结果。

class Solution {
public:
    int longestValidParentheses(string s) {
        if (s.size() <= 1)
            return 0;
        s = ')' + s;
        int len = s.size();
        int * dp = new int[len];
        int res = 0;
        
        dp[0] = 0;
        dp[1] = 0;
        for (int i = 2; i < len; ++i)
        {
            if (s[i] == '(')
                dp[i] = 0;
            else
            {
                if (s[i-1] == '(')
                    dp[i] = dp[i-2] + 2;
                else
                {
                    if (s[i-dp[i-1]-1] == '(')
                        dp[i] = dp[i-1] + 2 + dp[ i-dp[i-1]-2 ];
                    else
                        dp[i] = 0;
                }
            }
            res = max(res, dp[i]);
        }
        
        return res;
    }
};

方法2：栈

首先用一个变量start记录上次匹配失败的位置，初始为-1 。

用一个栈stk，遇到左括号，把其下标入栈。

遇到右括号，

1. 若栈为空，则不匹配了，更新start的值。

2. 若栈不为空，弹出一个元素，和右括号匹配。

此时再看栈，如果

2.1 栈为空，则目前形成了匹配的序列，长度为 i – start

2.2 栈不为空，右括号和弹出的元素匹配了，长度为 i- stk.top()

class Solution {
public:
    int longestValidParentheses(string s) {
        if (s.size() <= 1)
            return 0;
        stack<int> stk;
        int start = -1;
        int res = 0;
        for (int i = 0; i < s.size(); ++i)
        {
            if (s[i] == '(')
            {
                stk.push(i);
            }
            else
            {
                if (stk.empty())
                {
                    start = i;
                }
                else
                {
                    stk.pop();
                    if (stk.empty())
                    {
                        res = max(res, i-start);
                        
                    }
                    else
                    {
                        res = max(res,i-stk.top());
                    }
                }
            }
        }
        
        
        return res;
    }
};