剑指Offer面试题27题：二叉搜索树与双向链表
题目描述：输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。
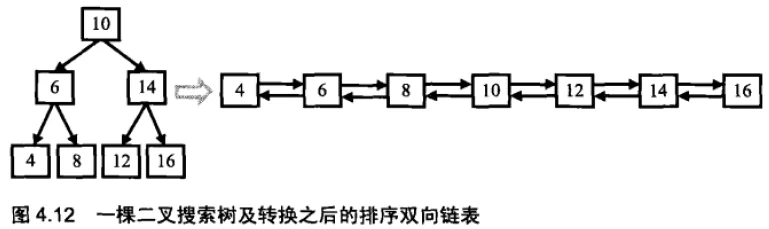
例如：
调整之后，节点的left指针相当于链表中的pred指针，节点的right指针相当于链表中的next指针。
在线提交代码网址：二叉搜索树与双向链表
二叉搜索树节点的定义
|
1 2 3 4 5 6 7 8 |
struct TreeNode { int data = 0; TreeNode * left = 0; TreeNode * right = 0; TreeNode(int data = 0) : data(data), left(0), right(0) {} }; |
解法1：中序遍历
对二叉搜索树进行中序遍历，节点的访问顺序正好就是有序的，也是最终得到的链表的顺序。要按照访问次序把节点连接起来，我们需要一个记录上一个节点的指针。这样，访问一个节点时，我们把上一个节点和目前访问的节点连接起来。
版本1：由中序遍历修改
中序遍历的思路为：递归处理左子树， 访问节点，递归处理右子树。我们需要修改的部分就是访问节点的代码，在访问时，把上一个节点和访问的节点链接起来。我们的递归函数如下：
|
1 2 3 4 |
void help(TreeNode * root, TreeNode * & pred) { } |
这个help函数，用于处理root为根的树，变为有序链表。第二个参数pred记录上一个访问的节点。
首先处理递归基，当root为空的时候，表示这个子树为空，不需要任何操作，直接返回。
|
1 2 3 4 5 6 7 |
void help(TreeNode * root, TreeNode * & pred) { if (root == 0) return; } |
接下来，按照中序遍历的思路，先递归处理左子树
|
1 2 3 4 5 6 7 |
void help(TreeNode * root, TreeNode * & pred) { if (root == 0) return; help(root->left, pred); //把左子树变为有序链表 } |
得益于递归的机制，第6行运行完毕后，左子树转换完毕，并且pred记录了上一个访问的节点。而我们马上就要访问的是root节点了，所以，接下来只要把他们（pred和root）连接到一起。
|
1 2 3 4 5 6 7 8 9 10 |
void help(TreeNode * root, TreeNode * & pred) { if (root == 0) return; help(root->left, pred); //把左子树变为有序链表 root->left = pred;//连接上一个访问的节点和目前访问的节点 pred->right = root;//连接上一个访问的节点和目前访问的节点 } |
这样pred和root节点就连接到了一起，root节点访问完毕。下面要更新上次访问的节点pred 为 root，这样，下次访问某个节点的时候pred就是记录上一个节点了
|
1 2 3 4 5 6 7 8 9 10 11 12 |
void help(TreeNode * root, TreeNode * & pred) { if (root == 0) return; help(root->left, pred); //把左子树变为有序链表 root->left = pred;//连接上一个访问的节点和目前访问的节点 pred->right = root;//连接上一个访问的节点和目前访问的节点 pred = root;//更新上一个访问的节点 } |
最后，递归处理右子树
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
void help(TreeNode * root, TreeNode * & pred) { if (root == 0) return; help(root->left, pred); //把左子树变为有序链表 root->left = pred; //连接上一个访问的节点和目前访问的节点 pred->right = root;//连接上一个访问的节点和目前访问的节点 pred = root;//更新上一个访问的节点 help(root->right, pred);//把右子树变为有序链表 } |
这样，help函数就写完了。最后写一个调用他的函数来实现题目需要的功能：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
TreeNode * BinaryTree2LinkedList(TreeNode * root) { if (!root) return 0; TreeNode head(0); //创建一个链表头节点 TreeNode * pred = &head; //pred初始为头节点 这样调用函数后，树转换成的链表和头节点是连在一起的 help(root, pred); //该语句完成后，root为根的树变成了链表，并连接到了pred（head）后面 head.right->left = 0; //处理完成后，再把我们的头节点去掉 这样链表就是完全由树转化来的了 return head.right; //返回的是树变为链表后的第一个节点 } |
版本2：中序遍历+建立链表分离
中序遍历的代码：
|
1 2 3 4 5 6 7 8 9 10 11 |
//方法4 中序遍历 template<typename F> void InOrderTraverse(TreeNode * root, F visit) { if (root) { InOrderTraverse(root->left, visit); visit(root); InOrderTraverse(root->right, visit); } } |
在visit函数里完成当前访问节点和上一个访问节点的连接，同样需要visit函数里面有一个记录上一个访问节点pred的变量。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
TreeNode * BinaryTree2LinkedList(TreeNode * root) { if (!root) return 0; TreeNode head(0); TreeNode * pred = &head; InOrderTraverse(root, [&pred](TreeNode * p){ pred->right = p; p->left = pred; pred = p; }); head.right->left = 0; return head.right; } |
方法2：递归
help函数的功能是把root为根的树变为链表，同时返回链表的头节点和尾节点（通过引用参数返回）
void help(TreeNode * root, TreeNode * & first, TreeNode * & last)
递归处理左子树后，把根节点和左子树链表的尾节点连接。
递归处理右子树后，把根节点和右子树链表的头节点相连。
由于first和last都是引用类型，在所有递归过程中他们只有一个，因此需要在函数中使用额外变量保存每次递归调用时的first和last。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
void help(TreeNode * root, TreeNode * & first, TreeNode * & last) { if (root == 0) { first = 0; last = 0; return; } TreeNode *resfirst = root; TreeNode *reslast = root; if (root->left) { help(root->left, first, last); //执行后，first是左子树的头节点，last是左子树的尾节点 resfirst = first; //更新头节点位置为左子树头节点 //连接root和左子树的尾节点 root->left = last; last->right = root; } if (root->right) { help(root->right, first, last); //执行后，first是右子树的头节点，last是右子树的尾节点 reslast = last; //更新尾节点位置为右子树尾节点 //连接root和右子树 root->right = first; first->left = root; } //函数返回后，first和last就是root为根的子树链表的头节点和尾节点 first = resfirst; last = reslast; return; } TreeNode * BinaryTree2LinkedList(TreeNode * root) { TreeNode * first; TreeNode * last; help(root, first, last); return first; } |
下面的版本利用返回值返回头节点和尾节点，来自 知乎@zearom32
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
pair<TreeNode * ,TreeNode * >BinaryTree2LinkedList(TreeNode * root) { if (!root) return make_pair(root,root); pair<TreeNode * ,TreeNode * > ans = make_pair(root,root); if (root->left){ pair<TreeNode * ,TreeNode * > tmp = BinaryTree2LinkedList_1(root->left); ans.first = tmp.first; root->left = tmp.second; root->left->right = root; } if (root->right){ pair<TreeNode * ,TreeNode * > tmp = BinaryTree2LinkedList_1(root->right); ans.second = tmp.second; root->right = tmp.first; root->right->left = root; } return ans; } |
支付宝打赏 
微信打赏
很好