雅乐网

Modularity的定义和公式推导可以参考Modularity的计算方法——社团检测中模块度计算公式详解 | 雅乐网

使用公式

$$Q = \sum_i{(\frac{e_i}{m} – (\frac{k_{C_i}}{2m})^2)} $$

其中， \(e_i\)表示社团 i 内部的边数，\(k_{C_i}\) 表示社团i内部所有点的度数之和，m表示图中边的个数。

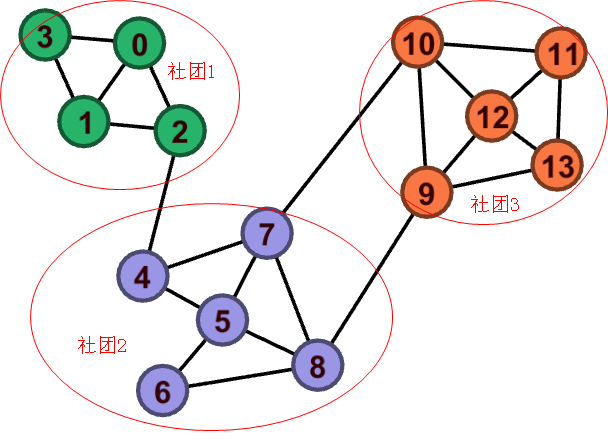
不妨先看一下手动的计算过程：

$$Q = \sum_i{(\frac{e_i}{m} – (\frac{k_{C_i}}{2m})^2)} $$

这个式子的i是要遍历所有的社团，例子中有3个社团，所以，Q就是3个部分的和，每个部分是

$$\frac{e_i}{m} – (\frac{k_{C_i}}{2m})^2$$

上图有23条边，m=23

先来计算社团1，这个社团 内部有5条边 ，所以 \(e_1 = 5\) ，内部结点4个，度数之和是 \(k_{C_1} = 11\)，这样求和的第一项就是

$$\frac{e_1}{m} – (\frac{k_{C_1}}{2m})^2 = \frac{5}{23} – (\frac{11}{2*23})^2 = \frac{339}{2116}$$

社团2和3也是这样计算：

$$\frac{e_2}{m} – (\frac{k_{C_2}}{2m})^2 = \frac{7}{23} – (\frac{17}{2*23})^2 = \frac{355}{2116}$$

$$\frac{e_3}{m} – (\frac{k_{C_3}}{2m})^2 = \frac{8}{23} – (\frac{18}{2*23})^2 = \frac{412}{2116}$$

最终的Q值就是这三个部分加起来：

$$Q =\frac{339}{2116} +\frac{355}{2116} + \frac{412}{2116}   = \frac{1106}{2116}=0.52268431$$

在代码中，我们的图是用边表示的，为了得到社团内部的边，可以遍历所有的边一次，每次看这条边的两个结点是否位于同一个社团内，是的话该社团内部边数+1

为了得到社团内部结点的度数之和，可以先得到图中所有结点的度，然后按照社团内部的点累加即可。

C++代码

下面的示例代码中，图是按照边表的形式存在一个 vector<pair<int,int>>  graph 中，社团文件存在 vector<vector<int>> communities; 中