雅乐网

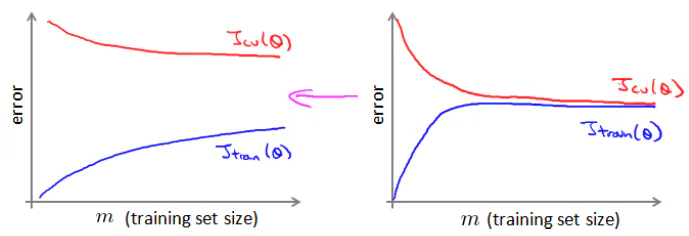
当训练集的规模很大时，可以帮助我们训练出更好的结果。但是，训练集规模的增大也带来了计算的代价非常大。

可以通过绘制学习曲线来判断大规模的训练集是否有必要。

梯度下降法的两个变种

假设我们的训练集中有100万个记录，在一般的梯度下降中，每次迭代更新时，都需要计算训练集误差的平方和，计算代价很大。下面的两种方法改进了这种每次需要计算所有训练集数据的算法。

随机梯度下降法（Stochastic grandient descent）

随机梯度下降算法中，每次使用单一的一个训练集数据来计算代价并更新参数。

$$cost(\theta, (x^{(i)}, y^{(i)})) = \frac{1}{2} (h_{\theta}(x^{(i)}) – y^{(i)})^2$$

在更新时，公式为：

$$\theta_j := \theta_j – \alpha (h_{\theta}(x^{(i)}) – y^{(i)}) x_j^{(i)}$$

下面是普通梯度下降算法（Batch Gradient descent）中的更新公式，可以比较一下：

$$\theta_j := \theta_j -\alpha \frac{1}{m} \sum_{i=0}^{m} \left( (h(x^{(i)}) – y^{(i)}) \cdot x_j\right)$$

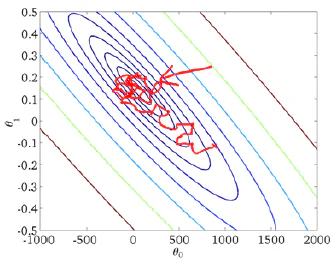
随机梯度下降中，每次使用1个训练集数据来更新参数，它的速度是很快的。但是它并不是每一步都朝着优化的方向进行的，只是总体上是逐渐优化。最终它可能在最小值附近徘徊。

微型批量梯度下降（MIni-Batch Gradient Descent）

微型批量梯度下降算法介于批量梯度下降算法和随机梯度下降算法之间。他每次使用b个训练实例来更新参数。通常b的范围是2-100 . 它的一个好处是可以采用向量化的方式并行计算，从而提高效率。

算法调试和收敛判断

怎么判断梯度下降是否在收敛呢？怎么选择学习率\(\alpha\) ？

在批量梯度下降中，可以让代价函数J随着迭代次数变化，画出图形，判断是否收敛。但是训练集规模很大时，这是不现实的。

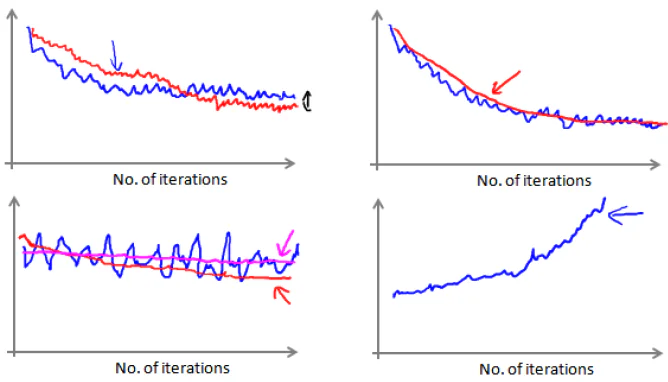
在随机梯度下降中，每次更新参数前计算代价，但画图时，一般选X次迭代的代价平均值。这样可以得到X次迭代的代价均值和X次迭代的次数的图形：

如果曲线的趋势是下降的，可以判定是正在收敛。否则，可能需要减小学习率，可以令学习率随着迭代次数增加而减小。例如：

$$\alpha = \frac{\text{const1}}{\text{iterationNumber + const2}}$$

高级主题

在线学习（Online Learning）

在线学习指的是要学习的数据来自数据流，而不是静态的训练集。数据流中的数据按照顺序一个接一个到来，不能回顾之前到来的数据。

例如物流公司网站，用户每次查询快递时，我们返回报价，有用户选择是否接受。每一次用户是否接受可以用来学习，以便预测下一次的用户是否接受某个报价。

在线学习的算法和随机梯度下降算法类似，对单一的实例进行学习。一旦一个数据的学习完成，这个数据就不再需要了。这种学习方式可以很快适应最近用户的习惯。

映射化简和数据并行（Map Reduce and Data Parallelism）

数据量很大时，有必要把数据分配给多个计算机计算，最后把各个结果汇总。这叫做映射化简。

例如需要对400个训练实例求和，可以分配4台机器，每台计算100个数据。最后把4个结果合并。

很多高级的线性代数库可以使用显卡的多核心来并行计算，因此算法的向量化非常重要。