本文介绍的数据结构英文是B-tree，中文写作B-树，其中 – 并不是减号，而是连接符，读作B树。
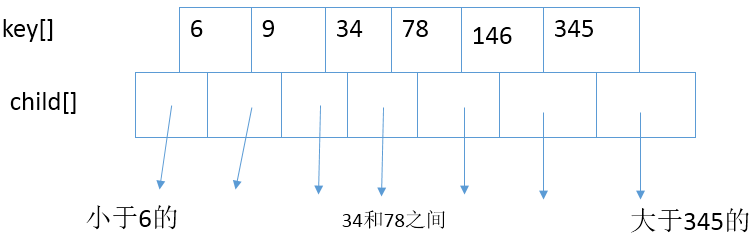
B-树是一种平衡搜索树，但它的每个结点包含的元素可以多于2个，因此并不是严格意义上的二叉树。
B-树的结点类似如下：
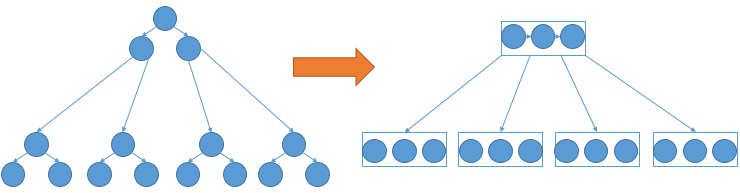
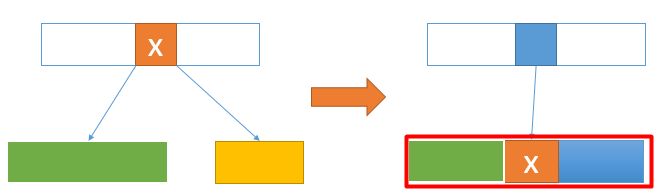
这可以看做二叉搜索树通过多层合并得到的
相比与二叉树，B树显得更矮，更胖。它的每个结点包含多个数据，这特别适合于对外存的访问。由于硬盘等设备访问速度和内存相比非常慢，而从硬盘读取1个数据和读取10个数据用时几乎一样，这非常适合使用B-树这种结构。每个结点数据很多，就可以从磁盘依次取出大量数据，矮的特点可以减少磁盘的IO次数。
定义
B-树的所有叶子结点都位于同一深度，同时对每个结点的分支数也有限制。一个m阶B-树满足
1. 每个结点的分支数最多m个，因此每个结点元素个数最多m-1个。
2. 除根节点外，每个结点的分支树最少 ⌈m/2⌉ 个（向上取整）。根节点例外，根节点可以只有2个分支。
这样，m阶B-树也可以叫做 (⌈m/2⌉ , m) -树 。
查找
B树的查找和二分查找类似，只不多这里是多分的。详见代码。
插入
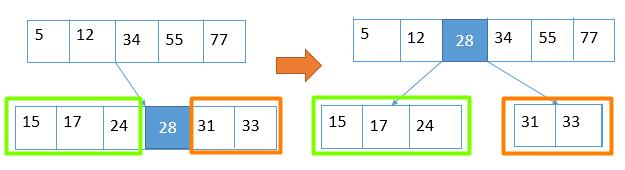
插入元素总是插入到叶节点，如果插入后节点数多余m-1，则要修复上溢。
发生上溢时，有m个结点，则分裂为左右两部分和中间轴点，左半部分有 m/2 个结点，中间1个结点，有半部分有⌈m/2⌉-1 个结点。 中间节点上升一层。父节点可能因此继续上溢。
删除
通过和中序后继交换，实现删除元素总是位于叶子。删除后如果分支数小于要求，则称下溢。
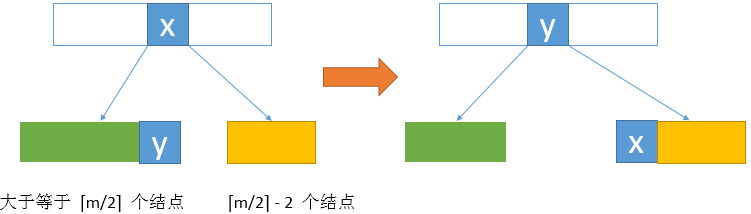
发生下溢时，可以先看左右兄弟是否可借出一个孩子
如果左右兄弟都不能借出，也就是都具有最少的结点，则可以进行合并。
C++实现
BTree.h
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 |
#include "Vector.h" #include "Queue.h" #define BTNodePosi(T) BTNode<T>* template <typename T> class BTNode { public: BTNodePosi(T) parent; Vector<T> key; Vector<BTNodePosi(T)> child; BTNode() : parent(NULL) { child.push_back(NULL); } BTNode(T e, BTNodePosi(T) lchild = NULL, BTNodePosi(T) rchild = NULL); }; template <typename T> BTNode<T>::BTNode(T e, BTNodePosi(T) lchild, BTNodePosi(T) rchild) { parent = NULL; key.insert(e); child.insert(0, lchild); child.insert(1, rchild); if (lchild) lchild->parent = this; if (rchild) rchild->parent = this; } template <typename T> class BTree { protected: int _size; int _order; BTNodePosi(T) _root; //根节点 BTNodePosi(T) _hot; void solveOverflow(BTNodePosi(T)); void solveUnderflow(BTNodePosi(T)); public: BTNodePosi(T) search(const T & e); bool insert(const T & e); bool remove(const T & e); void display(); BTree(int order) : _size(0), _order(order), _root(NULL), _hot(NULL) { } }; template <typename T> BTNodePosi(T) BTree<T>::search(const T & e) { BTNodePosi(T) p = _root; _hot = NULL; //反复循环直到到达外部结点 或者找到时直接return while (p) { //向量的search接口返回不大于e的最后一个元素 int n = p->key.search(e); //已经找到 if (p->key[n] == e) return p; //否则 下降一层 _hot = p; p = p->child[n+1]; } return NULL; } template <typename T> bool BTree<T>::insert(const T & e) { //不允许重复元素 if (search(e)) return false; //search执行后 _hot指向的是最终结点的父节点（search失败时指向外部结点的父节点 也就是叶子节点） BTNodePosi(T) p = _hot; if (!p) { //树为空的情况 p = new BTNode<T>; _root = p; p->key.push_back(e); p->child.push_back(NULL); ++_size; return true; } //树不为空时，将e插入到叶节点的适当位置 int n = p->key.search(e); p->key.insert(n+1, e); p->child.push_back(NULL); //叶节点的孩子是外部结点 全部为NULL 因此直接插入到最后面 ++_size; BTNodePosi(T) par; //插入结点后 从该结点到其祖先结点 依次检测是否上溢并修复 while (p && p->child.size() > _order) { par = p->parent; solveOverflow(p); p = par; } return true; } template <typename T> bool BTree<T>::remove(const T & e) { //找到e的位置 BTNodePosi(T) p = search(e); if (!p) return false; int n = p->key.search(e); //若e所在结点不是叶子结点 用它的中序意义后继替代它 之后只需删除位于叶子节点的那个后继 if (p->child[0]) { BTNodePosi(T) q = p->child[n+1]; while (q->child[0]) { q = q->child[0]; } p->key.put(n, q->key[0]); n = 0; p = q; } //现在待删除节点都位于叶子结点 开始删除 p->key.remove(n); p->child.remove(n); --_size; //删除元素后解决下溢问题 if (p != _root && p->child.size() < (_order+1)/2) { solveUnderflow(p); } return true; } //解决上溢问题 即pn的分支数超过了B树的阶_order template <typename T> void BTree<T>::solveOverflow(BTNodePosi(T) pn) { BTNodePosi(T) p = pn->parent; int n = (_order-1)/2; //n是最少结点数 //下面把pn结点分裂为lc和rc两个结点和中间一个只有一个元素的结点 //lc [0,n) 中间结点 [n] rc [n+1,size] int i; //左半部分 BTNodePosi(T) lc = new BTNode<T>; for (i = 0; i < n; ++i) { lc->key.push_back(pn->key[i]); if (i == 0) lc->child.put(0, pn->child[0]); else lc->child.push_back(pn->child[i]); } lc->child.push_back(pn->child[i]); for (i = 0; i < lc->child.size(); ++i) if (lc->child[i]) lc->child[i]->parent = lc; //右半部分 BTNodePosi(T) rc = new BTNode<T>; for (i = n+1; i < pn->key.size(); ++i) { rc->key.push_back(pn->key[i]); if (i == n+1) rc->child.put(0, pn->child[i]); else rc->child.push_back(pn->child[i]); } rc->child.push_back(pn->child[i]); for (i = 0; i < rc->child.size(); ++i) if (rc->child[i]) rc->child[i]->parent = rc; if (!p) { //上溢结点是树根节点的情况 p = new BTNode<T>; _root = p; } //把中间节点插入到pn的父节点 其左右指针指向lc和rc两部分 lc->parent = p; rc->parent = p; int n1 = p->key.search(pn->key[n]); p->key.insert(n1+1, pn->key[n]); p->child.put(n1+1, lc); p->child.insert(n1+2, rc); delete pn; } template <typename T> void BTree<T>::solveUnderflow(BTNodePosi(T) q) { //没有下溢则退出 if (q->child.size() >= (_order+1)/2) return; if (q == _root) { if (q->key.empty()) { //树根节点删除了最后一个元素变为空树的情况 _root = q->child[0]; delete q; } return; //树根节点最少可以是1个结点 没有下溢的问题 } BTNodePosi(T) p = q->parent; int n; for (n = 0; n < p->child.size(); ++n) { if (p->child[n] == q) break; } BTNodePosi(T) lc; BTNodePosi(T) rc; //q的左兄弟可以借出结点 if (n > 0 && p->child[n-1]->child.size() > (_order+1)/2) { lc = p->child[n-1]; q->key.insert(0, p->key[n-1]); q->child.insert(0, lc->child.last()); if (q->child[0]) q->child[0]->parent = q; p->key.put(n-1, lc->key.last()); lc->key.remove(lc->key.size() - 1); lc->child.remove(lc->child.size() - 1); return; } //q的右兄弟可以借出结点 if (n < p->child.size()-1 && p->child[n+1]->child.size() > (_order+1)/2) { rc = p->child[n+1]; q->key.push_back(p->key[n]); q->child.push_back(rc->child[0]); if (rc->child[0]) rc->child[0] = q; p->key.put(n, rc->key[0]); rc->key.remove(0); rc->child.remove(0); return; } //q的左右兄弟都不能借出 则合并 if (n > 0) { //有左兄弟时，与左兄弟合并 lc = p->child[n-1]; lc->key.push_back(p->key[n-1]); int i; for (i = 0; i < q->key.size(); ++i) { lc->key.push_back(q->key[i]); lc->child.push_back(q->child[i]); } lc->child.push_back(q->child[i]); p->key.remove(n-1); p->child.remove(n); delete q; } else { //否则和右兄弟合并 rc = p->child[n+1]; q->key.push_back(p->key[n]); int i; for (i = 0; i < rc->key.size(); ++i) { q->key.push_back(rc->key[i]); q->child.push_back(rc->child[i]); } q->child.push_back(rc->child[i]); p->key.remove(n); p->child.remove(n+1); delete rc; } //合并后，父节点的分支数减少，继续解决父节点的下溢问题 solveUnderflow(p); } template <typename T> class MyPrint { public: void operator()(T e) { cout << e << " "; } }; template <typename T> void BTree<T>::display() { if (!_root) return; MyPrint<T> visit; Queue<BTNodePosi(T)> q; BTNodePosi(T) x = _root; BTNode<T> endl1; q.enqueue(x); q.enqueue(&endl1); int i; while (!q.empty()) { x = q.dequeue(); if (!x) continue; if (x == &endl1) { if (q.size() > 0) q.enqueue(&endl1); printf("\n"); continue; } printf("#"); x->key.travser(visit); printf("#"); for (i = 0; i < x->child.size(); ++i) { q.enqueue(x->child[i]); } printf("----"); } } |
BTree.cpp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
#include <iostream> using namespace std; #include "BTree.h" int main() { BTree<int> bt(4); bt.insert(21); bt.insert(48); bt.insert(72); bt.insert(12); bt.insert(22); bt.insert(50); bt.insert(34); bt.insert(42); bt.insert(60); bt.insert(67); bt.insert(89); bt.insert(13); bt.display(); cout << "delete 50\n\n"; bt.remove(50); bt.display(); cout << "delete 72\n\n"; bt.remove(72); bt.display(); cout << "delete 89\n\n"; bt.remove(89); bt.display(); cout << "delete 67\n\n"; bt.remove(67); bt.display(); cout << "delete 48\n\n"; bt.remove(48); bt.display(); cout << "delete 60\n\n"; bt.remove(60); bt.display(); cout << "delete 42\n\n"; bt.remove(42); bt.display(); cout << "delete 22\n\n"; bt.remove(22); bt.display(); cout << "delete 34\n\n"; bt.remove(34); bt.display(); cout << "delete 21\n\n"; bt.remove(21); bt.display(); // int i; // for (i = 0; i < 30; ++i) // bt.insert(i); printf("233"); return 0; } |
支付宝打赏 
微信打赏