最新版完整代码：https://github.com/yalewoo/cpp-data-structure
二叉树
本文中的二叉树结点包含父指针，左右孩子指针，结点高度信息，具体数据结构为
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
//二叉树结点数据结构 template <typename T> class BinNode { public: T data; //该结点具体数据 BinNodePosi(T) parent; //父节点指针 BinNodePosi(T) lchild; //左孩子指针 BinNodePosi(T) rchild; //右孩子指针 enum RB_COLOR color; //颜色 在红黑树中使用 int height; //记录该结点高度 int horizontal_position; //记录中序遍历下该结点的序号，用于display显示 int distance_to_root; //记录到根节点的距离 用于display显示 int size(); //计算以该结点为根的二叉树结点个数（递归算法） BinNodePosi(T) insertAsLC(T const &); //插入左孩子 BinNodePosi(T) insertAsRC(T const &); //插入右孩子 BinNodePosi(T) succ(); //返回中序遍历时该结点的后继指针 //遍历算法 template <typename VST> void travPre_R(VST &); //先序遍历递归算法 template <typename VST> void travPre_I(VST &); //先序遍历基于栈的算法1 template <typename VST> void travPre_II(VST &); //先序遍历基于栈的算法2 template <typename VST> void travIn_R(VST &); //中序遍历递归算法 template <typename VST> void travIn_I(VST &); //中序遍历基于栈的算法 template <typename VST> void travPost_R(VST &); //后序遍历递归算法 template <typename VST> void travPost_I(VST &); //后序遍历基于栈的算法 template <typename VST> void travLevel(VST &); //层次遍历 基于队列 BinNode(T e, BinNodePosi(T) p); //构造二叉树，父节点p，节点内容e BinNode(); virtual ~BinNode(){} }; |
二叉树的数据结构
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
//二叉树数据结构 template <typename T> class BinTree { protected: int _size; //记录该二叉树结点个数 BinNodePosi(T) _root; //二叉树树根节点指针 virtual int updateHeight(BinNodePosi(T) x); //更新结点x的高度 void updateHeightAbove(BinNodePosi(T) x); //更新x以及x的所有祖先元素的高度 void updateDistanceToRoot(BinNodePosi(T) x); //更新x结点及其孩子距离根节点的距离 void calculatePosition(); //计算结点位置 结果存放在每个结点的horizontal_position和distance_to_root中 BinNodePosi(T) siblingOf(BinNodePosi(T) x); //返回结点x的兄弟结点 public: BinTree(BinNodePosi(T) root); BinTree(); virtual ~BinTree(); int size() const { return _size; } //返回树中结点个数 int height() const { return _root ? _root->height : 0; } //返回树的高度 bool empty() const { return !_root; } //判断树是否为空树 BinNodePosi(T) root() const { return _root; } //返回根节点指针 //拓扑连接 BinNodePosi(T) insertAsLC(BinNodePosi(T) x, T const & e); //把e作为x的左孩子插入 BinNodePosi(T) insertAsRC(BinNodePosi(T) x, T const & e); //把e作为x的右孩子插入 BinNodePosi(T) attachAsLC(BinNodePosi(T) x, BinTree<T>* & S); //把S作为x的左子树插入 BinNodePosi(T) attachAsRC(BinNodePosi(T) x, BinTree<T>* & S); //把S作为x的右子树插入 //删除x结点 virtual int remove(BinNodePosi(T) x); //将以x为根的子树从树中删去 BinNodePosi(T) secede(BinNodePosi(T) x); //树的遍历算法 template <typename VST> void travPre(VST &v) { _root->travPre_I(v); } //先序遍历 对每个节点执行v template <typename VST> void travIn(VST &v) { _root->travIn_I(v); } //中序遍历 template <typename VST> void travPost(VST &v) { _root->travPost_I(v); } //后序遍历 template <typename VST> void travLevel(VST &v) { _root->travLevel_I(v); } //层次遍历 //命令行直观显示二叉树 void display(); }; |
下面简单介绍一些重要接口的实现思路
高度
二叉树结点自身含有height成员变量，用于记录结点的高度信息，该信息在插入和删除时进行实时维护，主要通过updateHeightAbove函数来进行更新，该函数从下到上依次调用updateHeight函数对每个结点的高度进行更新。
在插入或者删除元素后，只会影响操作元素的祖先元素的高度，其余元素高度不受影响。采用从下到上的顺序，可以保证更新x结点高度时，x的孩子的高度已经得到更新。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
#define stature(p) ((p) ? (p)->height : -1) //该结点的高度 空节点高度为-1 //更新x结点的高度 template <typename T> int BinTree<T>::updateHeight(BinNodePosi(T) x) { return x->height = 1 + max(stature(x->lchild), stature(x->rchild)); } //更新x及其祖先结点高度 template <typename T> void BinTree<T>::updateHeightAbove(BinNodePosi(T) x) { while (x) { updateHeight(x); x = x->parent; } } |
结点个数
结点个数并不是直接记录在变量中，而是每次进行计算。计算采用递归的方法，结点个数 = 左子树结点个数 + 右孩子结点个数 + 1 ，递归基是叶子结点个数为1
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
/* 返回该结点为根的子树的结点个数 递归求解 return lc->size() + rc->size() + 1 叶子节点 return 1 */ template <typename T> int BinNode<T>::size() { int s = 1; if (lchild) s += lchild->size(); if (rchild) s += rchild->size(); return s; } |
树的结点操作
有插入左孩子，右孩子，左子树，右子树，分离子树，删除子树。
分离子树secede把子树从二叉树中分离，并返回子树的指针。
删除子树直接删除子树，并释放空间，返回的是删除的结点个数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
//分离子树 返回子树的树根 template <typename T> BinNodePosi(T) BinTree<T>::secede(BinNodePosi(T) x) { if (x->parent->lchild == x) x->parent->lchild = NULL; if (x->parent->rchild == x) x->parent->rchild = NULL; updateHeightAbove(x->parent); BinTree<T> * S = new BinTree<T>; S->_root = x; x->parent = NULL; S->_size = x->size(); _size -= S->size; return S; } //删除子树 释放空间 template <typename T> int removeTreeByRootNode(BinNodePosi(T) x) { if (x == NULL) return 0; int n = 1 + removeTreeByRootNode(x->lchild) + removeTreeByRootNode(x->rchild); delete x; return n; } |
遍历操作
见源代码
显示接口 display
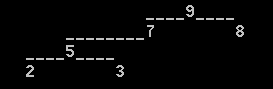
该函数可以在命令行界面下显示一棵二叉树。效果如图
显示时，结点的水平顺序就是中序遍历时结点的顺序，而垂直高度通过层次遍历得到。思路很简单，具体实现有点繁琐。见 二叉树的图形化显示
二叉搜索树
从二叉树派送而来，重写或增加 search 、insert和remove接口
search
二叉搜索树查找算法，该函数同时记录了查找结果的父节点，记录在hot成员变量中。这样可以用于insert时调用。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 |
#ifndef MY_BST_H #define MY_BST_H #include "Bintree.h" template <typename T> class BST : public BinTree<T> { public: BST(); virtual BinNodePosi(T) search(const T &); virtual BinNodePosi(T) insert(const T &); virtual bool remove(const T &); BinNodePosi(T) removeAt(BinNodePosi(T) x); protected: using BinTree<T>::_root; using BinTree<T>::_size; BinNodePosi(T) _hot; //parent of (x returned by search) void transplant(BinNodePosi(T) p, BinNodePosi(T) c); //move single node c to p void connect34(BinNodePosi(T) t1, BinNodePosi(T) t2, BinNodePosi(T) t3, BinNodePosi(T) st1, BinNodePosi(T) st2, BinNodePosi(T) st3, BinNodePosi(T) st4); }; template <typename T> BST<T>::BST() { _hot = NULL; } template <typename T> BinNodePosi(T) searchIn(BinNodePosi(T) root, const T & e, BinNodePosi(T) & hot) { BinNodePosi(T) x = root; hot = 0; while (x != NULL) { if (e == x->data) return x; hot = x; if (e < x->data) x = x->lchild; else x = x->rchild; } return x; } template <typename T> BinNodePosi(T) BST<T>::search(const T & e) { return searchIn(_root, e, _hot); } template <typename T> BinNodePosi(T) BST<T>::insert(const T & e) { BinNodePosi(T) p = BST<T>::search(e); if (p != NULL && p->data == e) //already exist { return p; } BinNodePosi(T) x = new BinNode<T>(e, _hot); if (_hot == NULL) //empty tree { _root = x; } else //insert as a leaf { if (e < _hot->data) _hot->lchild = x; else _hot->rchild = x; } ++_size; this->updateHeightAbove(x); return x; } //the called function should modify the lchild and rchild of c //meanwhile, children node of p not changed template <typename T> void BST<T>::transplant(BinNodePosi(T) p, BinNodePosi(T) c) { if (p == _root) { _root = c; if (c) c->parent = 0; return; } if (p->parent->lchild == p) p->parent->lchild = c; else p->parent->rchild = c; if (c) c->parent = p->parent; } //删除结点x 若有左右孩子，与中序后继交换再删 //返回实际删除的结点的替代者指针 _hot指向删除后实际删除节点替代者的父节点 template <typename T> BinNodePosi(T) BST<T>::removeAt(BinNodePosi(T) x) { BinNodePosi(T) suc; if (!x->lchild) //x has no lchild, just use rchild to replace x,including rchild==NULL { suc = x->rchild; _hot = x->parent; transplant(x, x->rchild); } //has lchild else if (!x->rchild) //no rchild ,move lchild to x { suc = x->lchild; _hot = x->parent; transplant(x, x->lchild); } else //two children { BinNodePosi(T) p = x->succ(); //p has no lchild suc = p->rchild; _hot = p->parent; T tmp = x->data; x->data = p->data; p->data = tmp; transplant(p, p->rchild); } --_size; this->updateHeightAbove(_hot); return suc; } template <typename T> bool BST<T>::remove(const T & e) { BinNodePosi(T) x = search(e); if (!x) return false; removeAt(x); delete x; return true; } template <typename T> void BST<T>::connect34(BinNodePosi(T) t1, BinNodePosi(T) t2, BinNodePosi(T) t3, BinNodePosi(T) st1, BinNodePosi(T) st2, BinNodePosi(T) st3, BinNodePosi(T) st4) { t1->lchild = st1; if (st1) st1->parent = t1; t1->rchild = st2; if (st2) st2->parent = t1; t3->lchild = st3; if (st3) st3->parent = t3; t3->rchild = st4; if (st4) st4->parent = t3; t2->lchild = t1; t1->parent = t2; t2->rchild = t3; t3->parent = t2; this->updateHeightAbove(t1); this->updateHeightAbove(t3); } #endif |
BST.cpp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
#include <iostream> using namespace std; #include "BST.h" template <typename T> class MyPrint { public: void operator()(T const &e) { cout << e << " "; } }; int main() { // MyPrint<int> visit; BST<int> b; // b.insert(8); // b.insert(3); // b.insert(7); // b.insert(9); // b.insert(11); // b.insert(5); // b.insert(51); // b.insert(2); // b.insert(1); // b.insert(88); // b.insert(64); // b.insert(67); // b.travIn(visit); // cout << endl << b.height() << endl; // b.remove(51); // b.travIn(visit); // cout << endl << b.height() << endl; // cout << endl; // b.remove(67); b.insert(7); b.insert(6); b.insert(5); b.insert(4); b.insert(3); b.insert(2); b.insert(1); b.display(); cout << endl << endl; return 0; } |
支付宝打赏 
微信打赏