常用数据结构C++实现(4)：AVL树

最后修改于 2016-01-15 发表于 2016-01-15 2,043 0

数据结构 ,

一般的二叉搜索树的高度并没有得到有效限制，在极端情况下，他甚至可以退化为一个链表。而对树高进行限制以达到O(logn)高度的二叉搜索树，又称为平衡搜索树。AVL树是最先发明的自平衡二叉查找树，它的名字来源于它的发明者 G.M. Adelson-Velsky 和 E.M. Landis 。

平衡搜索树因为树高控制在O(logn)的范围内，查找操作用时O(logn)。进行插入和删除操作时，可能会破坏树的平衡性质，需要进行重平衡操作（rebalance）。

定义

首先定义结点的平衡因子，等于左子树高度减去右子树高度。AVL树的每个结点的平衡因子取值只有-1, 0, 1三种取法，也就是说任意结点的左右孩子高度差不超过一。

AVL树的高度

为了说明AVL树的高度和结点数的关系，我们从相反的角度，考虑高度为h的AVL树最少包含多少个结点。

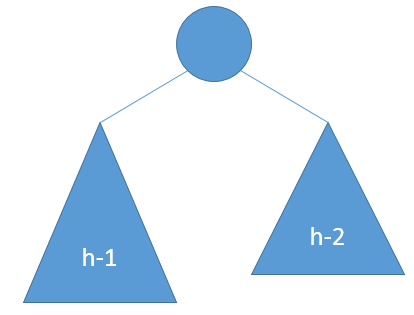
令高度为h的AVL树包含的最少结点是T(h)，则高度为h-1的AVL树最少结点是T(n-1)，高度为h-2的AVL树最少结点是T(n-2)。接下来用递归的思想来考虑如何得到一棵高度h的AVL树。

显然，树的左右孩子也必须是AVL树。由于总高度为h，因此左孩子或右孩子中的较大者高度为h-1，另一个孩子高度为h-1或h-2 ，由于我们要计算最少结点数，另一个孩子高度取h-2

scrn20160114150604

由此得到递推关系式： T(h) = T(h-1) + T(h-2) + 1 ，初始条件 T(1) = 1 ， T(2) = 2

对两边同时+1 ，得 T(h) + 1 = T(h-1)+1   +  T(h-2) + 1

令S(h) = T(h) + 1 , S(h) = S(h-1) + S(h-2)  ，S(1) = 2, S(2) = 3

对比斐波那契数列 0 1 1 2 3 5

可得 S(h) = F(h+2)

T(h) = F(h+2) – 1

而F(n)的通项中n在指数上，由此可得，节点数为n时，高度为O(logn)量级。

查找

AVL的查找可以直接使用BST的查找，算法不变。由于树高得到控制，查找时间复杂度为O(logn)

插入

插入后失去平衡的情况有4种，重平衡的过程也可以通过单旋和双旋来完成。

首先来看简单的单旋：

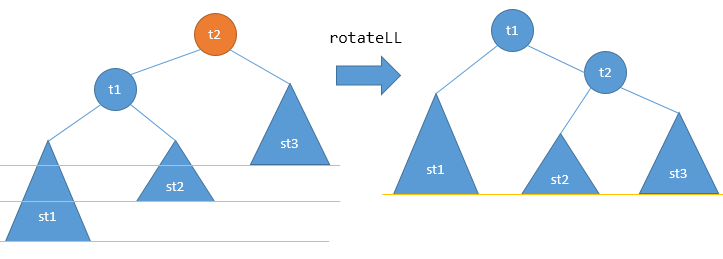
左左情况  rotateLL

某结点因为其左孩子的左子树插入导致失衡，在这里叫做rotateLL过程。

scrn20160114153718

代码如下

template <typename T>
void AVL<T>::rotateLL(BinNodePosi(T) t1, BinNodePosi(T) t2)
{
	//t2 --> st2
	t2->lchild = t1->rchild;

	//st2 --> t1
	if (t1->rchild)
		t1->rchild->parent = t2;

	//t1 --> t2
	t1->rchild = t2;

	//父节点 --> t1（树根情况）
	if (t2->parent == NULL)
	{
		t1->parent = NULL;
		this->_root = t1;

		t2->parent = t1;
		return;
	}

	//t1 --> 父节点
	t1->parent = t2->parent;

	//父节点 --> t1（非树根）
	if (t2->parent->lchild == t2)
		t2->parent->lchild = t1;
	else
		t2->parent->rchild = t1;

	//t2 --> t1
	t2->parent = t1;
}

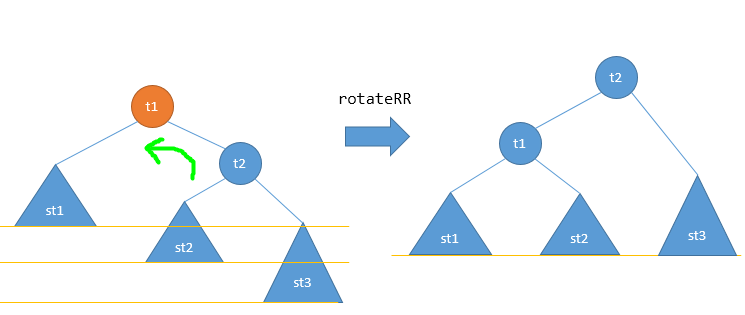
 右右情况 rotateRR

某结点因为其右孩子的右子树插入导致失衡，在这里叫做rotateRR过程。

scrn20160114154651

代码如下

template <typename T>
void AVL<T>::rotateRR(BinNodePosi(T) t2, BinNodePosi(T) t1)
{
	//t1 --> st2
	t1->rchild = t2->lchild;

	//st2 --> t1
	if (t2->lchild)
		t2->lchild->parent = t1;

	//t2 --> t1
	t2->lchild = t1;

	//父节点 --> t2（树根）
	if (t1->parent == NULL)
	{
		this->_root = t2;
		t2->parent = NULL;
		t1->parent = t2;
		return;
	}

	//t2 --> 父节点
	t2->parent = t1->parent;

	//父节点 --> t2（非树根）
	if (t1->parent->lchild == t1)
		t1->parent->lchild = t2;
	else
		t1->parent->rchild = t2;

	//t1 --> t2
	t1->parent = t2;
}

左右情况

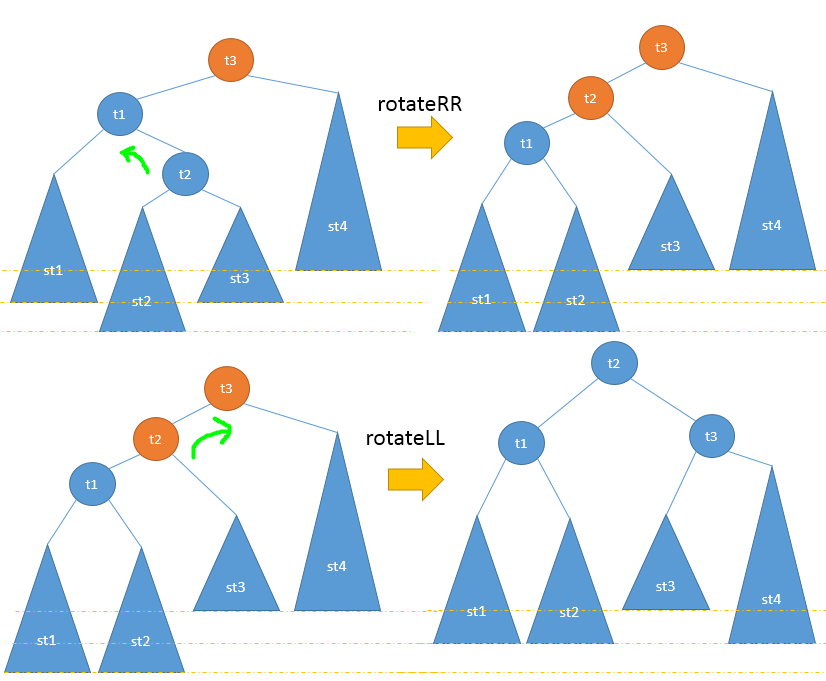
某结点的左孩子的右子树插入导致失衡。此时需要进行两次单旋。

scrn20160114162140

右左情况

某结点的右孩子的左子树插入导致失衡。此时需要进行两次单旋。

此情况与左右情况对称，此处略去。

使用旋转重平衡

template <typename T>
void AVL<T>::insertFixUp(BinNodePosi(T) p)
{
	BinNodePosi(T) q;
	q = tallerChild(p);
	q = tallerChild(q);

	if (p->lchild && q == p->lchild->lchild)
	{
		rotateLL(q->parent, p);
	}
	else if (p->rchild && q == p->rchild->rchild)
	{
		rotateRR(q->parent, p);
	}
	else if (p->lchild && q == p->lchild->rchild)
	{
		rotateRR(q, q->parent);
		this->updateHeightAbove(q->lchild);
		rotateLL(p->lchild, p);
	}
	else
	{
		rotateLL(q, q->parent);
		this->updateHeightAbove(q->rchild);
		rotateRR(p->rchild, p);
	}

	this->updateHeightAbove(p);
}

3+4重构

上面通过旋转来使树恢复平衡的过程比较繁琐。实际上可以通过观察发现，不管怎么旋转，调整后的树仍然要满足中序遍历下的大小关系。

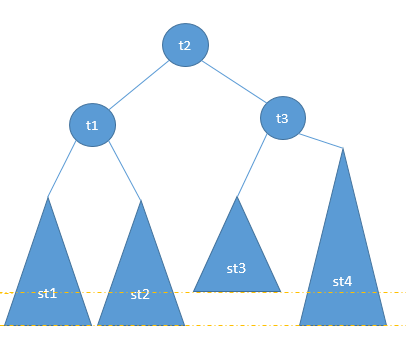
例如上面的左右情况，旋转最终的结果的拓扑连接总是下图这样：

scrn20160114163338

因此，直接将这3个结点，4个子树连接成上图的样子，既方便又明了。

template <typename T>
void AVL<T>::insertFixUp2(BinNodePosi(T) p)
{
	BinNodePosi(T) q;
	BinNodePosi(T) mid;
	mid = tallerChild(p);
	q = tallerChild(mid);

	BinNodePosi(T) par = p->parent;
	enum {ROOT, LEFT, RIGHT} ptoc;
	if (p->parent)
	{
		if (p == p->parent->lchild)
			ptoc = LEFT;
		else
			ptoc = RIGHT;
	}
	else
		ptoc = ROOT;
		
	BinNodePosi(T) t1;
	BinNodePosi(T) t2;
	BinNodePosi(T) t3;
	BinNodePosi(T) st1;
	BinNodePosi(T) st2;
	BinNodePosi(T) st3;
	BinNodePosi(T) st4;

	if (p->lchild && q == p->lchild->lchild)
	{
		t1 = q;
		t2 = q->parent;
		t3 = p;
		st1 = q->lchild;
		st2 = q->rchild;
		st3 = mid->rchild;
		st4 = p->rchild;
	}
	else if (p->rchild && q == p->rchild->rchild)
	{
		t1 = p;
		t2 = mid;
		t3 = q;
		st1 = p->lchild;
		st2 = mid->lchild;
		st3 = q->lchild;
		st4 = q->rchild;
	}
	else if (p->lchild && q == p->lchild->rchild)
	{
		t1 = mid;
		t2 = q;
		t3 = p;
		st1 = mid->lchild;
		st2 = q->lchild;
		st3 = q->rchild;
		st4 = p->rchild;
	}
	else
	{
		t1 = p;
		t2 = q;
		t3 = mid;
		st1 = p->lchild;
		st2 = q->lchild;
		st3 = q->rchild;
		st4 = mid->rchild;
	}

	switch (ptoc)
	{
		case ROOT : _root = t2; break;
		case LEFT : par->lchild = t2; break;
		case RIGHT : par->rchild = t2; break;
	}
	t2->parent = par;

	connect34(t1, t2, t3, st1, st2, st3, st4);
}
template <typename T>
void AVL<T>::connect34(BinNodePosi(T) t1, BinNodePosi(T) t2, BinNodePosi(T) t3, BinNodePosi(T) st1, BinNodePosi(T) st2, BinNodePosi(T) st3, BinNodePosi(T) st4)
{
	t1->lchild = st1; if (st1) st1->parent = t1;
	t1->rchild = st2; if (st2) st2->parent = t1;
	t3->lchild = st3; if (st3) st3->parent = t3;
	t3->rchild = st4; if (st4) st4->parent = t3;
	t2->lchild = t1; t1->parent = t2;
	t2->rchild = t3; t3->parent = t2;

	this->updateHeightAbove(t1);
	this->updateHeightAbove(t3);
}

删除

template <typename T>
bool AVL<T>::remove(const T & e)
{
	BinNodePosi(T) x = search(e);
	if (!x) return false;

	removeAt(x);

	BinNodePosi(T) p = _hot;
	BinNodePosi(T) q;
	while (p != NULL)
	{
		q = p;
		p = p->parent;
		if (!AvlBalanced(q))
		{
			insertFixUp2(q);
		}
	}

	return true;
}

 

完整代码：https://github.com/yalewoo/cpp-data-structure

如果文章对你有帮助，欢迎点赞或打赏（金额不限）。你的打赏将全部用于支付网站服务器费用和提高网站文章质量，谢谢支持。

版权声明:

本文由 原创，商业转载请联系作者获得授权。
非商业转载请注明作者 或 雅乐网 ，并附带本文链接：
https://www.yalewoo.com/data_structure_cpp_4_avl_tree.html

上一篇：

下一篇：

与 , 相关的文章

我要评论

验证码*： 9 + 0 =