常用数据结构C++实现(5)：伸展树

最后修改于 2016-01-17 发表于 2016-01-16 1,877 0

数据结构 ,

伸展树也是一种平衡二叉搜索树，但它的平衡是在平均意义下的。伸展树中n次操作，每次的均摊复杂度是O(logn) 。而单独的一次操作，可能达到O(n)的复杂度。那么，与AVL相比，伸展树的优势又在哪里呢？

伸展树中，每次会把访问到的结点通过单旋和双旋移动到树的根部，这样下次在访问该结点时，就可以极大地节省时间。也就是说，伸展树可以很好地满足数据访问的局部性。假设在一段时间内，访问的元素有k个，k << n ，则伸展树会达到比AVL更好的性能。

此外，伸展树与AVL相比，对平衡的约束较小，因此更加容易实现。

查找和伸展

伸展树中，查找到相应元素后，通过旋转把该结点移动到根部，这个过程为splay(x) 。

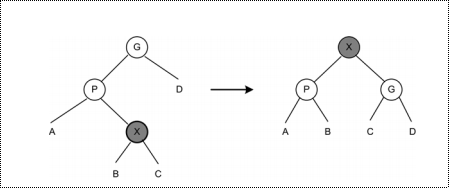
这个过程也要用到AVL中的旋转，如果待上升结点为x，要看x的父节点和爷爷结点。具体有2种情况：

1. 2010031717354266

这种情况逐层旋转，x绕p旋转，然后绕g旋转。这和AVL的双旋一致。

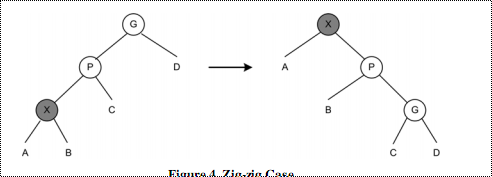
2.2010031717355587

这种情况先绕G旋转，再绕P旋转。这种情况和AVL中不一样。

c++实现

https://github.com/yalewoo/cpp-data-structure

SplayBinTree.h

#include "BST.h"
template <typename T>
class SplayBinTree : public BST<T>
{
protected:
	using BST<T>::updateHeightAbove;
	using BST<T>::_root;
	using BST<T>::_hot;
	BinNodePosi(T) splay(BinNodePosi(T) v);

	void rotateLL(BinNodePosi(T) p, BinNodePosi(T) q);
	void rotateRR(BinNodePosi(T) p, BinNodePosi(T) q);
	void connect34(BinNodePosi(T) t1, BinNodePosi(T) t2, BinNodePosi(T) t3, BinNodePosi(T) st1, BinNodePosi(T) st2, BinNodePosi(T) st3, BinNodePosi(T) st4);
public:
	BinNodePosi(T) search(const T & e);
	BinNodePosi(T) insert(const T & e);
	bool remove(const T & e);
};

template <typename T>
BinNodePosi(T) SplayBinTree<T>::splay(BinNodePosi(T) v)
{
	BinNodePosi(T) p;
	BinNodePosi(T) mid;
	BinNodePosi(T) q;

	BinNodePosi(T) t1;	
	BinNodePosi(T) t2;	
	BinNodePosi(T) t3;	
	BinNodePosi(T) st1;	
	BinNodePosi(T) st2;	
	BinNodePosi(T) st3;	
	BinNodePosi(T) st4;	

	BinNodePosi(T) par;
	enum {ROOT, LEFT, RIGHT} ptoc;

	while ((q = v) && (mid = v->parent) && (p = v->parent->parent))
	{
		par = p->parent;

		if (par)
		{
			if (p == par->lchild)
				ptoc = LEFT;
			else
				ptoc = RIGHT;
		}
		else
			ptoc = ROOT;

		if (p->lchild && q == p->lchild->lchild)
		{
			t1 = q;
			t2 = q->parent;
			t3 = p;
			st1 = q->lchild;
			st2 = q->rchild;
			st3 = mid->rchild;
			st4 = p->rchild;

			t1->rchild = t2; t2->parent = t1;
			t2->lchild = st2; if (st2) st2->parent = t2;
			t2->rchild = t3; t3->parent = t2;
			t3->lchild = st3; if (st3) st3->parent = t3;

			switch (ptoc)
			{
				case ROOT : _root = t1; break;
				case LEFT : par->lchild = t1; break;
				case RIGHT : par->rchild = t1; break;
			}
			t1->parent = par;

			updateHeightAbove(t3);
		}
		else if (p->rchild && q == p->rchild->rchild)
		{
			t1 = p;
			t2 = mid;
			t3 = q;
			st1 = p->lchild;
			st2 = mid->lchild;
			st3 = q->lchild;
			st4 = q->rchild;

			t1->rchild = st2; if (st2) st2->parent = t1;
			t2->lchild = t1; t1->parent = t2;
			t2->rchild = st3; if (st3) st3->parent = t2;
			t3->lchild = t2; t2->parent = t3;

			switch (ptoc)
			{
				case ROOT : _root = t3; break;
				case LEFT : par->lchild = t3; break;
				case RIGHT : par->rchild = t3; break;
			}
			t3->parent = par;

			updateHeightAbove(t1);
		}
		else if (p->lchild && q == p->lchild->rchild)
		{
			t1 = mid;
			t2 = q;
			t3 = p;
			st1 = mid->lchild;
			st2 = q->lchild;
			st3 = q->rchild;
			st4 = p->rchild;
			
			switch (ptoc)
			{
				case ROOT : _root = t2; break;
				case LEFT : par->lchild = t2; break;
				case RIGHT : par->rchild = t2; break;
			}
			t2->parent = par;

			this->connect34(t1, t2, t3, st1, st2, st3, st4);
		}
		else
		{
			t1 = p;
			t2 = q;
			t3 = mid;
			st1 = p->lchild;
			st2 = q->lchild;
			st3 = q->rchild;
			st4 = mid->rchild;
			
			switch (ptoc)
			{
				case ROOT : _root = t2; break;
				case LEFT : par->lchild = t2; break;
				case RIGHT : par->rchild = t2; break;
			}
			t2->parent = par;

			this->connect34(t1, t2, t3, st1, st2, st3, st4);
		}

	}
	if ((q = v) && (mid = v->parent) && !(p = v->parent->parent))
	{
		if (q == mid->lchild)
			this->rotateLL(q, mid);
		else
			this->rotateRR(q, mid);

		updateHeightAbove(mid);
	}

	return v;
}
template <typename T>
BinNodePosi(T) SplayBinTree<T>::search(const T & e)
{
	BinNodePosi(T) x = searchIn(_root, e, _hot);
	if (!x)
		splay(_hot);
	else
		splay(x);
	return x;
}
template <typename T>
BinNodePosi(T) SplayBinTree<T>::insert(const T & e)
{
	BinNodePosi(T) x = search(e);
	if (x)
		return x;

	BinNodePosi(T) v = new BinNode<T>(e, NULL);
	BinNodePosi(T) p = _root;
	_root = v;
	if (p && p->data < e)
	{
		p->parent = v;
		v->lchild = p;
		v->rchild = p->rchild;
		if (p->rchild) p->rchild->parent = v;
		p->rchild = 0;
	}
	else if (p)
	{
		p->parent = v;
		v->rchild = p;
		v->lchild = p->lchild;
		if (p->lchild) p->lchild->parent = v;
		p->lchild = 0;
	}
	updateHeightAbove(p);
	updateHeightAbove(v);

	return v;
}
template <typename T>
bool SplayBinTree<T>::remove(const T & e)
{
	BinNodePosi(T) v = search(e);
	if (!v)
		return false;

	BinNodePosi(T) p = v->succ();
	BinNodePosi(T) oldleft = v->lchild;

	if (v->lchild) v->lchild->parent = 0;
	if (v->rchild) v->rchild->parent = 0;
	delete v;

	if (!p)
	{
		_root = oldleft;
		return true;
	}

	splay(p);

	_root = p;
	p->parent = 0;
	p->lchild = oldleft;
	if (p->lchild) p->lchild->parent = p;

	return true;
}
template <typename T>
void SplayBinTree<T>::rotateLL(BinNodePosi(T) p, BinNodePosi(T) q)
{

	q->lchild = p->rchild;
	if (p->rchild)
		p->rchild->parent = q;

	p->rchild = q;


	if (q->parent == NULL)
	{
		p->parent = NULL;
		this->_root = p;

		q->parent = p;
		return;
	}

	p->parent = q->parent;
	if (q->parent->lchild == q)
		q->parent->lchild = p;
	else
		q->parent->rchild = p;

	q->parent = p;
}
template <typename T>
void SplayBinTree<T>::rotateRR(BinNodePosi(T) p, BinNodePosi(T) q)
{

	q->rchild = p->lchild;
	if (p->lchild)
		p->lchild->parent = q;

	p->lchild = q;
	if (q->parent == NULL)
	{
		this->_root = p;
		p->parent = NULL;
		q->parent = p;
		return;
	}


	p->parent = q->parent;

	if (q->parent->lchild == q)
		q->parent->lchild = p;
	else
		q->parent->rchild = p;

	q->parent = p;
}

template <typename T>
void SplayBinTree<T>::connect34(BinNodePosi(T) t1, BinNodePosi(T) t2, BinNodePosi(T) t3, BinNodePosi(T) st1, BinNodePosi(T) st2, BinNodePosi(T) st3, BinNodePosi(T) st4)
{
	t1->lchild = st1; if (st1) st1->parent = t1;
	t1->rchild = st2; if (st2) st2->parent = t1;
	t3->lchild = st3; if (st3) st3->parent = t3;
	t3->rchild = st4; if (st4) st4->parent = t3;
	t2->lchild = t1; t1->parent = t2;
	t2->rchild = t3; t3->parent = t2;

	updateHeightAbove(t1);
	updateHeightAbove(t3);
}

SplayBinTree.cpp

#include <iostream>
#include <cstdlib>

#include "SplayBinTree.h"

using namespace std;

int main()
{
	SplayBinTree<int> b;

	for (int i = 32; i >=1; --i)
	{
		b.insert(i);
	}
	
	// b.remove(32);
	// b.remove(4);

	char c;
	for (int i = 32; i >=1; --i)
	{
		b.display();

		cout << "Press Enter to Search " << i;
		while ((c = getchar()) != '\n')
			;
		b.search(i);
		system("cls");
	}
	b.search(1);

	b.display();

	return 0;
}

 

如果文章对你有帮助，欢迎点赞或打赏（金额不限）。你的打赏将全部用于支付网站服务器费用和提高网站文章质量，谢谢支持。

版权声明:

本文由 原创，商业转载请联系作者获得授权。
非商业转载请注明作者 或 雅乐网 ，并附带本文链接：
https://www.yalewoo.com/data_structure_cpp_5_splay_binary_tree.html

上一篇：

下一篇：

与 , 相关的文章

我要评论

验证码*： 1 + 0 =