逻辑回归(Logistic Regression)
逻辑回归虽然带有“回归”两个字,实际上却是分类问题,此时要预测的值y是离散的。例如判断一封邮件是否是垃圾邮件,判断肿瘤是恶性还是良性。
先从二元逻辑回归问题开始,也就是y的值只有0和1两种取法。
假说模型
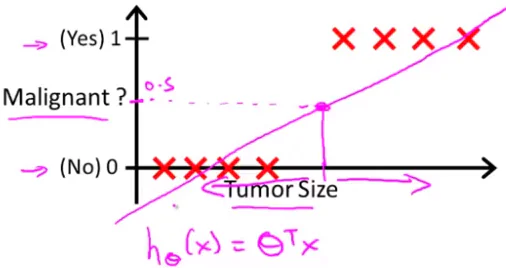
假设我们采用之前线性回归的模型
$$h(x) = \theta^T x$$
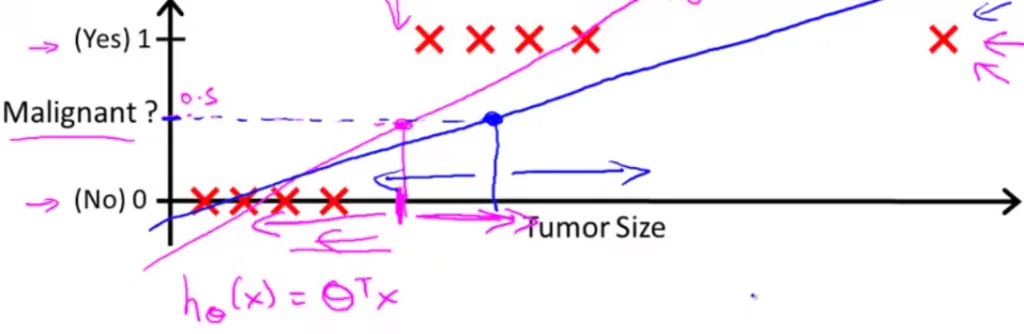
线性拟合后,我们用h(x)大于0.5预测1,小于0.5预测0 。看上去此时它工作良好。但是,如果新加一个数据点
这会导致预测错误。可以看出线性回归的模型不再适合这个分类问题了,因为此时h(x)的值并不是0到1之间,而可能大于1.
因此在逻辑回归中,我们需要引入新的模型
$$h(x) = g(\theta^T x)$$
其中的g代表逻辑函数(logistic function),其中最常用的一种叫做S 形函数(Sigmoid function),其定义如下:
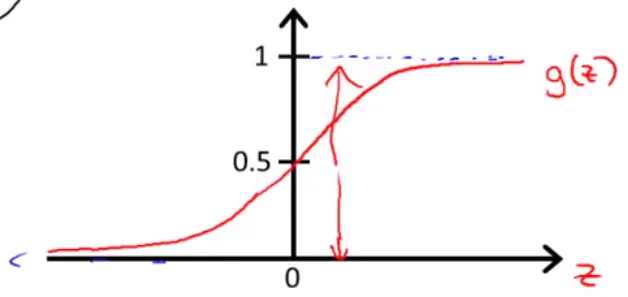
$$g(z) = \frac{1}{1 + e^{-z}}$$
当z趋于负无穷时,g(z)趋向0;当z趋于正无穷时,g(z)趋向于1;当z=0时,g(z) = 0.5 。g(z)的图形大致 如下:
合起来就可以得到用于逻辑回归的模型
$$h_\theta(x) = \frac{1}{1 + e^{- \theta^T x}}$$
此时h(x)给出的结果是x对应的输出y=1的概率,也就是
$$h(x) = P(y=1 | x; \theta)$$
当h(x)大于0.5时,我们预测结果为1;当h(x)小于0.5时,预测结果为0。根据上面的图形
\(\theta^T x > 0\)时,对应h(x) > 0.5,应该预测结果为1;
\(\theta^T x < 0\)时,对应h(x) < 0.5,应该预测结果为0;
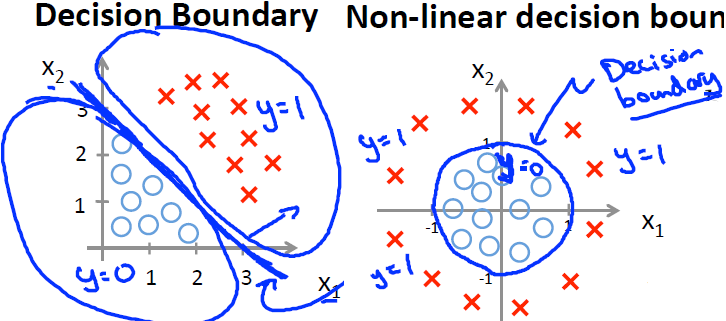
决策边界(Decision Boundary)
模型中的分界线,将预测为1的区域和预测为0的趋于分成两部分。
代价函数(Cost Function)
在线性回归模型中的代价函数是每个实例误差的平方和
$$J(\theta_0, \theta_1, …, \theta_n) = \frac{1}{2m} \sum_{i=0}^{m} (h(x^{(i)}) – y^{(i)})^2$$
但是逻辑回归中,h(x)的形式变了。如果沿用上述公式,将导致J()是一个非凸函数,不利于我们找最值。因此,代价函数也需要重新定义:
$$J(\theta) = \frac{1}{m} \sum_{i = 1}^{m} \left( Cost(h(x^{(i)}), y^{(i)})\right)$$
其中
$$Cost(h(x), y) = \begin{cases}
-log(h(x)), & \text{if $y$ = 1} \\
-log(1-h(x)), & \text{if $y$ = 0} \\
\end{cases}$$
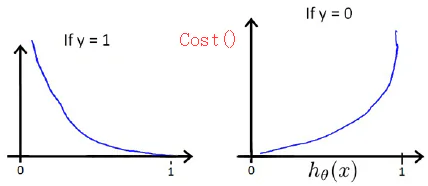
h(x)和Cost(h(x), y)之间的关系如下:
当y=1时,h(x)越接近1,Cost越小;h(x)越接近0,Cost越大。
当y=0时,h(x)越接近1,Cost越大;h(x)越接近0,Cost越小。
因此,Cost的定义是合理的,估计误差越大,代价就越大。
为了把Cost从两种情形合并为一种,可以写成如下的形式:
$$Cost(h(x), y) = -y log(h(x)) – (1-y) log(1-h(x))$$
代入到代价函数中得到:
$$J(\theta) = – \frac{1}{m} \sum_{i = 1}^{m} \left( y^{(i)} log(h(x^{(i)})) + (1-y^{(i)}) log\left(1-h(x^{(i)})\right) \right)$$
之后我们便可以使用梯度下降算法来求使代价函数最小的参数值了
$$\theta_j := \theta_j – \alpha \frac{\partial}{\partial \theta_j} J(\theta)$$
求导后得到(待推导)
$$\theta_j := \theta_j – \frac{\alpha}{m} \sum_{i=1}^{m}\left( \left(h(x^{(i)}) – y^{(i)}\right) x_j^{(i)} \right)$$
这看上去和线性回归中的更新规则相似,但却是不同的。因为其中的h(x)函数不一样。
线性回归中的假设函数
$$h(x) = \theta^T x$$
逻辑回归中的假设函数
$$h(x) = g(\theta^T x) = \frac{1}{1 + e^{- \theta^T x}}$$
调用matlab中的高级算法
可以调用 共轭梯度(Conjugate Gradient),局部优化法(Broyden fletcher goldfarb shann,BFGS)和有限内存局部优化法(LBFGS)等高级算法。只需要告诉计算机 如何求 \(J(\theta)\) 和 \(\frac{\partial }{\partial \theta_j} J(\theta)\) 。
这些高级算法的特点:不必手动选择学习率\(\alpha\) ,收敛速度很快; 实现复杂,不过库中已经实现了。
下面是一个例子:
我们要来求使\(J(\theta)\)最小的参数值。需要实现一个函数
function [jVal, gradient] = costFunc(theta)
jVal = (theta(1) - 5)^2 + (theta(2) - 5)^2;
gradient = zeros(2, 1);
gradient(1) = 2 * (theta(1) - 5);
gradient(2) = 2 * (theta(2) - 5);
end
调用
options = optimset('GradObj', 'on', 'MaxIter', 100);
>> initialTheta = zeros(2, 1);
>> [optTheta, functionVal, exitFlag] = fminunc(@costFunc, initialTheta, options)
Local minimum found.
Optimization completed because the size of the gradient is less than
the default value of the function tolerance.
<stopping criteria details>
optTheta =
5
5
多分类问题
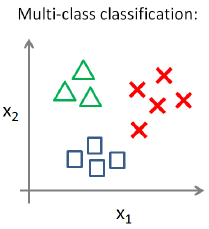
多分类问题中的y输出多余2个值,一种可能的情况如下:
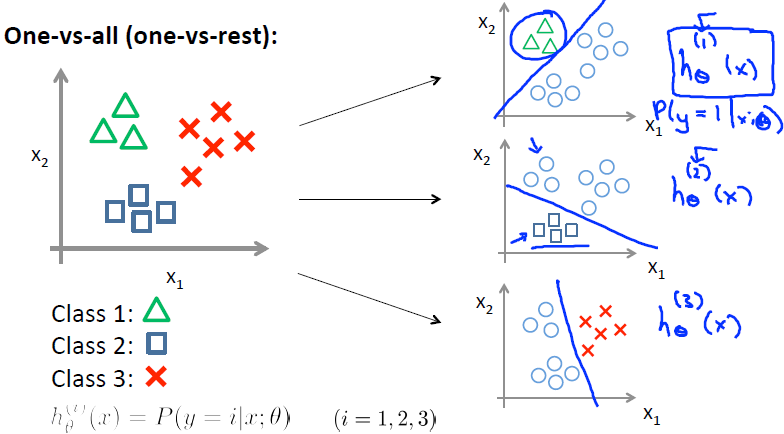
使用一对多(One-vs-All)的方法可以解决这个问题。在一对多方法中,每次我们把数据分为y=某个和y=其他。
例如,先分成y=1和其他两部分,得到 \(h^{(1)}(x)\)
类似,y=2时可以得到 \(h^{(2)}(x)\)
最后,我们得到一系列假说
$$h^{(i)}(x)$$
在多分类问题时,我们把每个假说函数运行一遍,求出其中最大的概率。
正则化(Regularization)
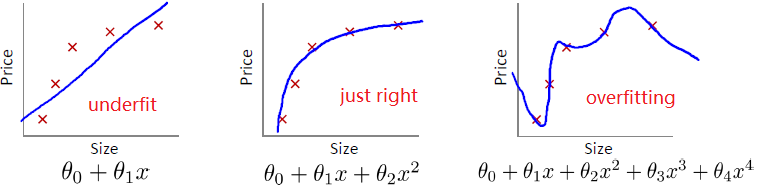
过拟合(Overfitting)
第一个用线性来拟合,显然不够准确,这称为欠拟合。
第二个看上去刚刚好。
第三个用过高次数的多项式,虽然完美拟合了训练集中的每个数据,但显然预测新数据时并不可靠。这称为过拟合。
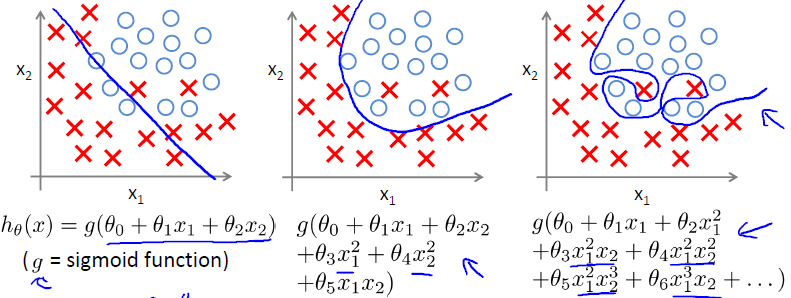
分类问题中也有类似的问题
正则化代价函数
上面回归问题中过拟合的模型是
$$h(x) = \theta_0 + \theta_1 x1 + \theta_2 x_2^2 + \theta_3 x_3^3 + \theta_4 x_4^4$$
如果减少 \(\theta_3\) 和 \(\theta_4\)的值,可以考虑修改代价函数,给它们添加一些惩罚。修改后的代价函数如下:
$$J(\theta) = \frac{1}{2m} \left( \sum_{i=1}^{m} (h(x^{(i)}) – y^{(i)})^2 + 999\theta_3^2 + 999\theta_4^2 \right)$$
这样会使\(\theta_3\) 和 \(\theta_4\)的值减小很多。
假设我们有很多特征,不知道要缩小哪一个,可以采用下面的办法
$$J(\theta) = \frac{1}{2m} \left( \sum_{i=1}^{m} (h(x^{(i)}) – y^{(i)})^2 + \lambda \sum_{j=1}^{n} \theta_j^2 \right)$$
根据惯例,我们不对\(\theta_0\)进行惩罚。
其中 \(\lambda\)又叫做正则化参数(Regularization Parameter)。如果正则化参数太大,则会把所有参数最小化,导致近似直线,造成欠拟合。
正则化线性回归
代价函数
$$J(\theta) = \frac{1}{2m} \left( \sum_{i=1}^{m} (h(x^{(i)}) – y^{(i)})^2 + \lambda \sum_{j=1}^{n} \theta_j^2 \right)$$
更新规则
$$\theta_0 := \theta_0 – \alpha \frac{1}{m} \sum_{i=1}^{m} \left( (h(x^{(i)}) – y^{(i)}) x_0^{(i)} \right)$$
$$\theta_j := \theta_j – \alpha \left( \frac{1}{m} \sum_{i=1}^{m} (h(x^{(i)}) – y^{(i)}) x_0^{(i)} + \frac{\lambda}{m} \theta_j \right) , \text{for j = 1, 2, … , n}$$
把上式变形一下
$$\theta_j := \theta_j(1 – \alpha \frac{\lambda}{m}) – \alpha \frac{1}{m} \sum_{i=1}^{m} \left( (h(x^{(i)}) – y^{(i)}) x_j^{(i)} \right)$$
对比不正则化的线性回归,正则化线性回归的梯度下降中,每\(\theta\)的因数从1变为\(1 – \alpha \frac{\lambda}{m}\),因此\(\theta\)要额外缩小了一点。
使用正规方程也可以求解正则化线性回归问题,公式是
正则化逻辑回归
代价函数
$$J(\theta) = – \left[ \frac{1}{m} \sum_{i = 1}^{m} \left( y^{(i)} log(h(x^{(i)})) + (1-y^{(i)}) log\left(1-h(x^{(i)})\right) \right) \right] + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2$$
通过求导得出的梯度下降算法更新规则
$$\theta_0 := \theta_0 – \alpha \frac{1}{m} \sum_{i=1}^{m} \left( (h(x^{(i)}) – y^{(i)}) x_0^{(i)} \right)$$
$$\theta_j := \theta_j – \alpha \left(\frac{1}{m} \sum_{i=1}^{m} (h(x^{(i)}) – y^{(i)}) x_j^{(i)} + \frac{\lambda}{m} \theta_j \right) , \text{for j = 1, 2, … , n}$$
这看上去和线性回归一样,但是h(x)是不同的。
仍然可以使用fminuc等函数来求解,只需修改参数的更新规则。
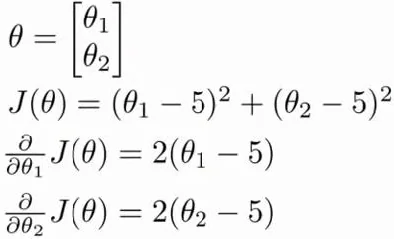
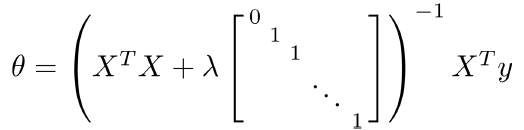
 支付宝打赏
支付宝打赏  微信打赏
微信打赏
不是归一化线性/逻辑回归, 是正则化线性/逻辑回归. 归一化是mean normalization, 正则化是regularization. 两个不是一回事
对的对的 谢谢指正 已经修改了
已经修改了