雅乐网

数据结构中的堆和程序语言中的堆的意义并不相同，这里的堆是一种数据结构。二叉堆可以分为最大堆和最小堆，这里介绍最大堆。在最大堆中，结点的值满足堆的性质：除了根节点外，所有结点都不会比它的父节点大。

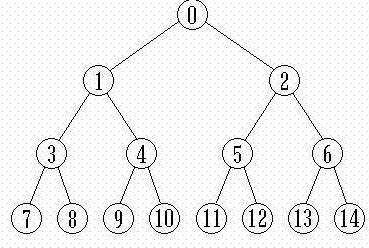
可以看到，逻辑上的堆是二叉树，但堆的物理结构却是数组，这得益于完全二叉树的性质：

假设数组下标从0开始，二叉树中父亲和孩子的关系可以方便的通过下标计算得到（图中数字是下标而不是实际的值）

#define PARENT(i) ((i-1)/2)
#define LCHILD(i) (2*i+1)
#define RCHILD(i) (2*(i+1))

堆的主要操作

最大堆主要有三种操作：获取最大值，向堆中插入元素并保持堆的性质，删除最大值并保持堆的性质。

由于最大堆的定义，堆中元素最大值必定出现在树根，也就是下标0的地方，因此获取最大值可以在常数时间完成。

插入元素

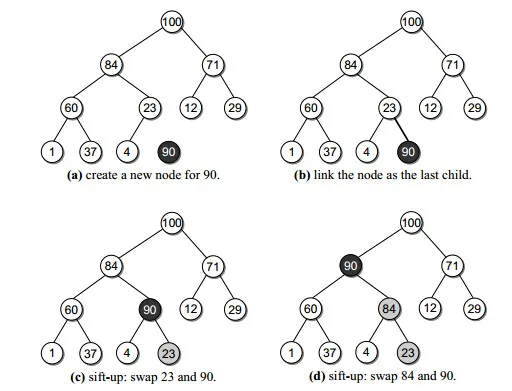
插入元素插入数组尾部，这样仍然保持了完全二叉树的性质，但堆序性可能得到破坏。

这可以通过比较新插入元素和它的父节点元素的值，如果新插入的元素更大，则要与父节点交换。交换后，新的结点和新的父节点又面临相同的问题。反复执行到新结点比父节点小或者到根节点，这个过程就可以停止。

由于完全二叉树树高为O(logn)，在最坏情况下，需要O(logn)的时间完成插入过程。

但是，由于树中大部分结点都位于底层，实际插入的过程中，甚至只需要常数时间，上滤过程就可以终止。

删除最大元素

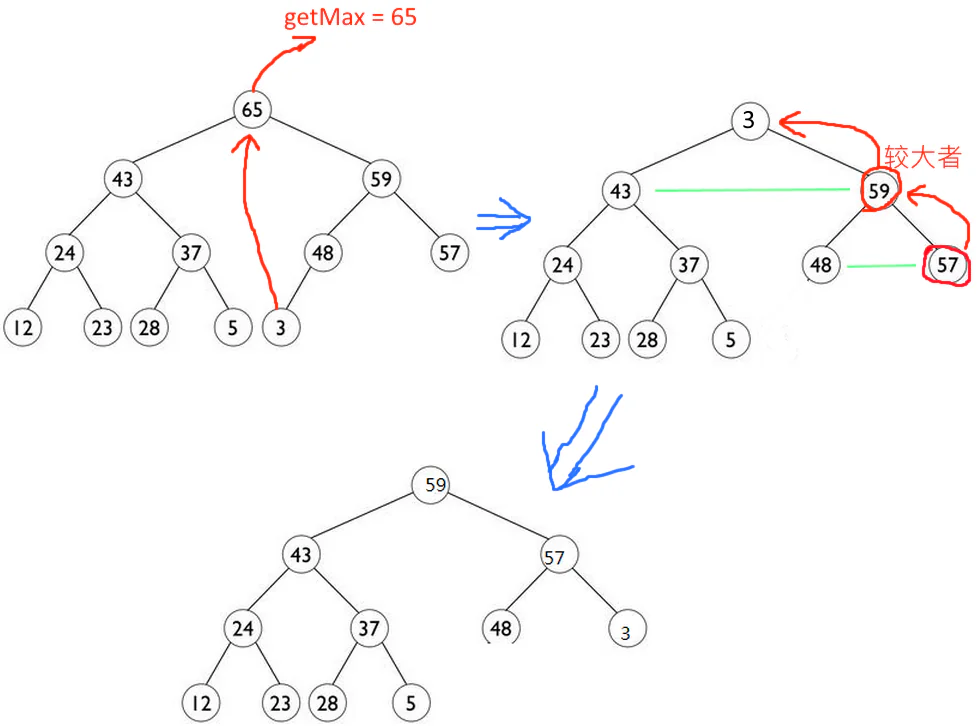
最大元素位于树根处，为了保持完全二叉树的形状，将尾部元素移到根节点处，然后通过下滤过程来重新调整使之满足堆序性。

每次比较根节点和两个孩子节点中的较大者，若不满足堆序性就进行交换。

在最坏情况下，时间复杂度也是树高，即O(logn)

批量建堆

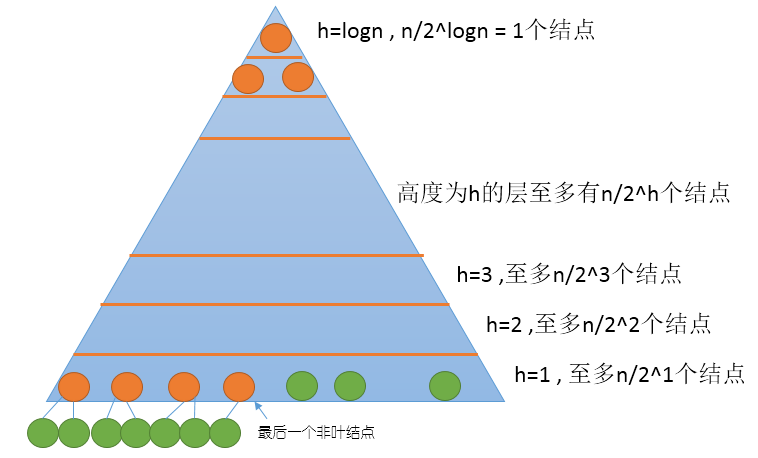
批量建堆采取从下到上逐渐下滤的过程，左右的叶子结点都看做一个满足堆序性的堆。只需要从最后一个非叶节点开始，从下到上，从右到左的对每个结点进行下滤。这需要遍历n/2个结点，每个结点所用时间是该节点的高度。由于树中大部分结点位于底部，所以大部分结点高度都很小。

实际上，完全二叉树中，最底层元素最多n/2个，而倒数第二层元素最多n/4个，依次类推。高度为h的元素最多有n/(2^h)个元素，每个元素下滤用时为h ，依次求和

$$ \sum_{h=0}^{h=lgn} \frac{n}{2^h} h = n \sum_{h=0}^{h=lgn} \frac{h}{2^h} <  n \sum_{h=0}^{\infty} h (\frac{1}{2})^h$$

因为 $$ \sum_{h=0}^{\infty} h x^h = x \sum_{h=0}^{\infty} h x^{h-1} = x \sum_{h=0}^{\infty} \frac{d(x^h)}{dx} = x \frac{d (\sum_{h=0}^{\infty} x^h )}{dx} = x \frac{d (\frac{1}{1-x})}{dx} = \frac{x}{(1-x)^2}$$

因此$$\sum_{h=0}^{\infty} h (\frac{1}{2})^h = \frac{\frac{1}{2}}{(1-(\frac{1}{2})^2)} = 2$$

因此时间复杂度为 O(n)

堆排序

类似于选择排序的过程，只不过这次选择前半部分的最大值不再直接遍历，而是通过堆来快速得到，然后用时O(logn)重新调整堆。这样总的用时为O(nlogn)。

c++实现

#include <cstdio>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <iostream>

using std::cout;
using std::endl;

/*       0     
     1      2
   3   4  5   6 */
#define PARENT(i) ((i-1)/2)
#define LCHILD(i) (2*i+1)
#define RCHILD(i) (2*(i+1))

template <typename T>
class Heap{
	bool isnew;
	T *_elem;
	int capacity;	//堆的最大容量
	int size;	//现有元素个数
	void percolateUp(int i);	//上滤调整
	void percolateDown(int i);	//下滤调整
public:
	Heap(int n){
		capacity = n;
		_elem = new T[n];
		isnew = true;
		size = 0;
	}
	Heap(int *a, int n)
	{
		_elem = a;
		isnew = false;
		capacity = n;
		size = n;
	}
	~Heap(){
		if (isnew)
			delete[] _elem;
	}
	T delMax();
	T getMax();
	void insert(T a);
	void heapify();
	void heapSort();
	void display();
};

//删除最大元素并返回
template <typename T>
T Heap<T>::delMax()
{
	if (size == 0)
		return 0;
	int max = _elem[0];
	_elem[0] = _elem[--size];
	percolateDown(0);
	return max;
}
//返回最大元素
template <typename T>
T Heap<T>::getMax()
{
	if (size == 0)
		return 0;
	return _elem[0];
}
//向堆中插入一个元素
template <typename T>
void Heap<T>::insert(T a)
{
	_elem[size++] = a;
	percolateUp(size-1);
}
//下滤调整
template <typename T>
void Heap<T>::percolateDown(int i)
{
	int tmp = _elem[i];
	
	int m = i;
	do
	{
		int l = LCHILD(i);
		int r = RCHILD(i);
		if (l >= size)
			break;
		if (l == size-1)	//处理只有左孩子或没有孩子的情况
			m = l;
		else if (_elem[l] > _elem[r])
			m = l;
		else
			m = r;

		if (_elem[m] > tmp)
		{
			_elem[i] = _elem[m];
			i = m;
		}
		else
			break;
	}
	while (m < size && _elem[m] > tmp);

	_elem[i] = tmp;
}
//上滤调整
template <typename T>
void Heap<T>::percolateUp(int i)
{
	int tmp = _elem[i];
	int p = PARENT(i);
	while (i > 0 && _elem[p] < tmp)
	{
		_elem[i] = _elem[p];
		i = p;
		p = PARENT(i);
	}
	_elem[i] = tmp;
}
//批量建堆 用时O(n)
template <typename T>
void Heap<T>::heapify()
{
	int i = PARENT(size-1);
	for (; i >= 0; --i)
	{
		percolateDown(i);
	}
}
//堆排序
template <typename T>
void Heap<T>::heapSort()
{
	heapify();
	while (size > 0)
	{
		_elem[size-1] = delMax();
	}
}
//屏幕输出堆中元素
template <typename T>
void Heap<T>::display()
{
	for (int i = 0; i < size; ++i)
		cout << " " << _elem[i] << " ";
}

int main()
{
	const int N = 100;
	int a[N];
	int i;
	srand((int)time(0));	//生成随机数组
	for (i = 0; i < N; i++)
		a[i] = rand() % N;
	for (int i = 0; i < N; ++i)
		printf("%d ", a[i]);
	putchar('\n');

	//进行堆排序
	Heap<int> h(a, N);
	h.heapSort();

	for (int i = 0; i < N; ++i)
		printf("%d ", a[i]);
	
	return 0;
}