雅乐网

本文是学堂在线计算几何课程 凸包一章的部分学习笔记。如果要求编程判断一个点是否在三角形（三个点）内部。

可以看出，如果点在三角形的内部，沿着三边走一圈，这个点相对于行进路径始终保持相同方向（图中一直在左边）； 如果点在三角形的外部，沿着三条边走一圈，会有不同的结果（图中左右左）。 这样，只要判断点和直线的相对位置就可以了。

点的数据结构表示

这里的代码使用c++，每个点包含x坐标和y坐标，还增加了一个构造函数。

struct Point{
	int x;
	int y;
	Point(int a, int b) :x(a), y(b){ }
};

点P可以用一个Point对象表示，三角形用三个Point对象表示。按照上面的思路，我们先要解决判断点和直线的位置关系。

点和直线的位置关系

注意这里的直线是有方向的，例如P点在AB的坐标，但在BA的右边。

叉积的正负和两条线的夹角

这里可以使用向量的叉积，两个向量的叉积是这样定义的： 向量积 a x b = (^n) * |a| * |b| * sin<a, b>, 其中^n是同时垂直于a/b且符合右手定则的单位向量。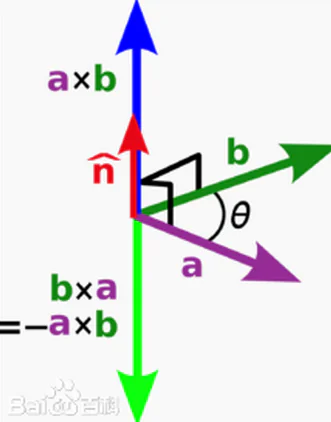

如果我们把^n忽略，只取数值的结果，AB × AP = |AB| * |AP| * sin∠PAB P在AB的左边，则∠PAB在0°到180°之间   sin∠PAB > 0 P在AB右边时，则∠PAB在-180°到0°之间 sin∠PAB < 0 因此，我们只要用AB和AP的叉积的正负，就可以判断P和AB的相对位置(AP相对AB是顺时针还是逆时针旋转)。

叉积的计算公式

这里有一个三维向量叉积的定义： \( \overrightarrow a = (x_1, y_1, z_1) , \overrightarrow b = (x_2, y_2, z_2) ,\)

$$ \overrightarrow a × \overrightarrow b = \begin{vmatrix} i & j & k \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ \end{vmatrix} $$

如果是二维向量，可以把第三维看做0 \( \overrightarrow a = (x_1, y_1,0) , \overrightarrow b = (x_2, y_2,0) ,\)

$$ \overrightarrow a × \overrightarrow b = \begin{vmatrix} i & j & k \\ x_1 & y_1 & 0 \\ x_2 & y_2 & 0 \\ \end{vmatrix} $$

$$ = (x_1y_2 – x_2y_1) k $$

AB向量的坐标是(b.x-a.x, b.y-a.y) ，AP向量的坐标是(p.x-a.x, p.y-a.y)

AB × AP = (b.x – a.x)(p.y – a.y) – (b.y – a.y)(p.x – a.x)

这样就得到了计算叉积的函数

int cross(const Point &a, const Point &b, const Point &p)
{
	return (b.x - a.x)*(p.y - a.y) - (b.y - a.y)*(p.x - a.x);
}

使用这个就可以得到判断点和直线位置关系的函数 判断P是否在AB的左边

bool toLeft(const Point &a, const Point &b, const Point &p)
{
	return cross(a, b, p) > 0;
}

inTriangleTest

根据上面的思路，对三角形的三边判断三次，就可以得到点是否在三角形内部了

bool inTriangle(const Point &p, const Point &a, const Point &b, const Point &c)
{
	bool res = toLeft(a, b, p);
	if (res != toLeft(b, c, p))
		return false;
	if (res != toLeft(c, a, p))
		return false;
	if (cross(a, b, c) == 0)	//ABC is in one line
		return false;
	return true;
}

注意，这里三角形退化的情况下判断结果是不在内部。

测试

测试了两个点

#include <cstdio>
#include <iostream>
using namespace std;

struct Point{
	int x;
	int y;
	Point(int a, int b) :x(a), y(b){ }
	friend ostream& operator<<(ostream &os, Point &p);
};

int cross(const Point &a, const Point &b, const Point &p)
{
	return (b.x - a.x)*(p.y - a.y) - (b.y - a.y)*(p.x - a.x);
}

bool toLeft(const Point &a, const Point &b, const Point &p)
{
	return cross(a, b, p) > 0;
}

bool inTriangle(const Point &p, const Point &a, const Point &b, const Point &c)
{
	bool res = toLeft(a, b, p);
	if (res != toLeft(b, c, p))
		return false;
	if (res != toLeft(c, a, p))
		return false;
	if (cross(a, b, c) == 0)	//ABC is in one line
		return false;
	return true;
}

ostream& operator<<(ostream &os, Point &p)
{
	os << "(" << p.x << ", " << p.y << ") " ;
	return os;
}

int main()
{
	Point A(1, 1);
	Point B(6, 3);
	Point C(4, 7);

	Point P(4, 1);
	if (inTriangle(P, A, B, C))
		cout << P << "is in Trinagle "<<A<<B<<C;
	else
		cout << P << "is not in Trinagle "<<A<<B<<C;

	printf("\n");

	Point Q(4, 5);
	if (inTriangle(Q, A, B, C))
		cout << Q << "is in Trinagle "<<A<<B<<C;
	else
		cout << Q << "is not in Trinagle "<<A<<B<<C;
	return 0;
}