快速排序通常是在实际应用中排序的最好算法,虽然在最坏情况下它的时间复杂度是O(n^2),但是在平均情况下,它的时间复杂度是O(nlogn),并且它的常数因子非常小,因此效率极高。
下面的描述中对数组a中的[lo,hi)进行排序。([lo,hi)表示一个前闭后开的下标范围,包含元素a[lo],…a[hi-1],不包含a[lo],共有hi-lo个元素)
思想
快速排序使用了分治的思想,它的主要步骤如下:
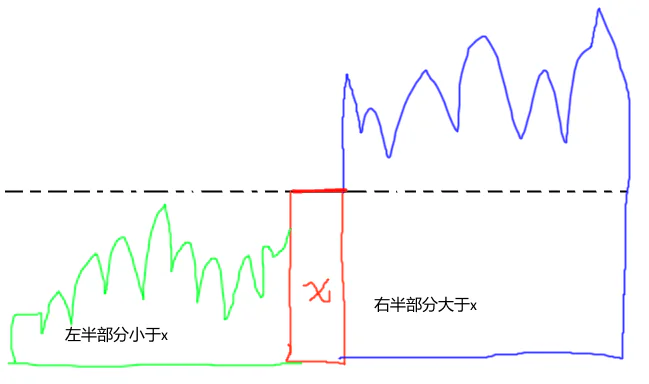
1. 选取一个元素x,并以这个元素为基础,把数组分成左右两个部分,其中左半部分都小于x,右半部分都大于x 。当然,等于x的部分归于左边和右边都可以。
2.递归的快速排序左半部分
3.递归的快速排序右半部分
因为x的位置就是最终排序后正确的位置,所以两次递归后不需要合并结果,左右分别排序好后整个数组自然就是有序的了。
主算法代码
根据上面的步骤,可以很简单的写出快速排序的步骤
void quicksort(int a[], int lo, int hi)
{
int mid;
mid = partition(a, lo, hi);
quicksort(a, lo, mid);
quicksort(a, mid+1, hi);
}
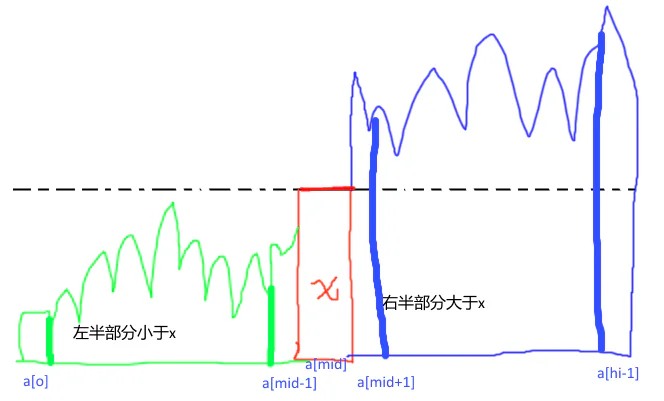
调用partition之后,[lo,mid)都小于x,[mid,mid+1)等于x,[mid+1, hi)大于x ,因此只需要递归的排序左右两个部分即可。
当数组中只有1个元素的时候,它就是平凡的有序,这时候需要退出递归,因此需要加上一句来处理递归基。
最终的快速排序函数如下:
void quicksort(int a[], int lo, int hi)
{
int mid;
if (hi - lo < 2) //元素个数小于2的时候 已经有序
return;
mid = partition(a, lo, hi);
quicksort(a, lo, mid);
quicksort(a, mid+1, hi);
}
划分
快速排序的关键在于划分,也就是上面的partition函数,该函数返回一个mid值,并原地将数组调整为左中右三部分。
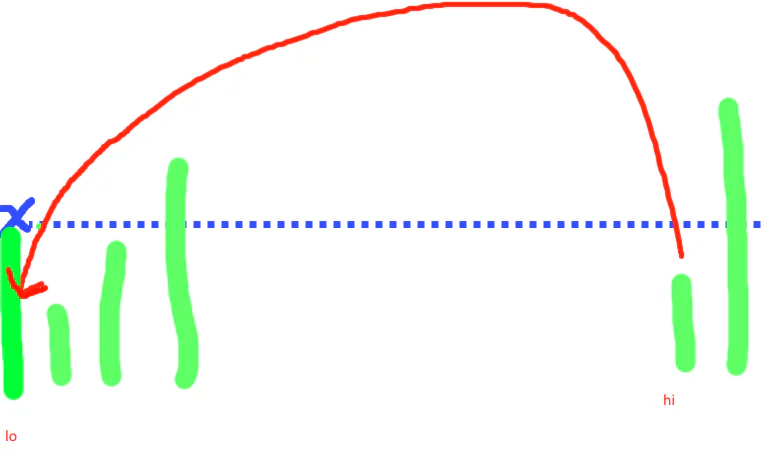
我们选取a[l0]作为x,尝试把数组分成小于x和大于等于x的两部分。使用lo和hi当做指针,分别从左边和右边遍历数组。
首先我们把a[lo]保存起来,
int partition(int a[], int lo, int hi)
{
int x = a[lo];
}
然后a[lo]就相当于一个空位,这时候我们从最右边出发,由于最右边元素是a[hi-1]所以这里我们先把hi减一。然后在while里面hi向左移动,我们知道右半部分应该大于等于x,因此只要hi>lo并且a[hi] >= x的情况下,我们一直递减hi,直到发现a[hi] < x,那么a[hi]元素应该属于左边才行,这时候我们把a[hi]复制到a[lo]的位置。
int partition(int a[], int lo, int hi)
{
int x = a[lo];
--hi;
while (hi > lo && a[hi] >= x)
--hi;
a[lo] = a[hi];
}
我们看这个while循环,跳出的时候如果hi>lo不满足 ,那么跳出后的a[lo]=a[hi]可以正确的移动元素。
如果是因为hi>lo而跳出循环,那么执行的是a[lo]=a[hi]相当于自己等于自己,对数组没有影响。
之后,a[hi]就相当于一个空位了,这时候我们转入左边,在lo < hi的情况下递增lo,直到找到a[lo]大于x,这时候我们把a[lo]移动到a[hi]处
int partition(int a[], int lo, int hi)
{
int x = a[lo];
--hi;
while (hi > lo && a[hi] >= x)
--hi;
a[lo] = a[hi];
while (lo < hi && a[lo] < x)
++lo;
a[hi] = a[lo];
}
然后我们在转入右边,递减hi 。可以看出右边和左边是交替进行的,我们可以把这两个while写进一个大的while里面。那么这个整体while的条件是什么呢?
在比较和复制的过程中,lo不断前进,hi不断减小,那么当lo<hi不成立的时候就可以停止了
int partition(int a[], int lo, int hi)
{
int x = a[lo];
--hi;
while (lo < hi)
{
while (hi > lo && a[hi] >= x)
--hi;
a[lo] = a[hi];
while (lo < hi && a[lo] < x)
++lo;
a[hi] = a[lo];
}
}
我们看大的while循环,每次循环执行后,lo前面的元素都<x, hi后面的元素都>=x ,而且a[lo]是一个空位
因此循环终止的时候lo==hi,这时候lo前面的元素小于x 后面的元素都大于等于x,这时候我们需要把最初备份的轴点x移动到a[lo]处就完成了划分。
我们的最终划分算法代码如下:
int partition(int a[], int lo, int hi)
{
int x = a[lo];
--hi;
while (lo < hi)
{
while (hi > lo && a[hi] >= x)
--hi;
a[lo] = a[hi];
while (lo < hi && a[lo] < x)
++lo;
a[hi] = a[lo];
}
a[lo] = x;
return lo;
}
划分选取元素的改进
快速排序的效率取决于每次把数组分成两个部分的时候是否平均,如果每次差不多分成一样大小的两个区间,那么递归的二分树就会矮胖矮胖,效率也会变高。
因此一种改进就是随机选取一个元素作为x,而不是每次选取a[lo] 。这种改进只需要在最开始吧a[lo]和选取的x互换位置,就可以仍然按照上面的代码来运行。
性能
首先划分partition的时间复杂度是O(n)。
在最坏情况下,假设每次都划分产生的两部分都有一部分是0,那么会导致时间复杂度达到O(n^2)。
幸运的是,只要两部分的划分是常数比例,即使是99:1 那么产生的递归树的深度也只有logn的级别。
在平均情况下,假设元素出现的概率相同。每次划分为[0,k]和[k+1,n],其中k的各个取值是等概率的。
假设总算法耗时T(n),递归左边耗时 T(k) ,右边耗时T(n-k-1),有
T(n) = O(n) + T(k) + T(n-k-1)
所有的情况下,k可以取值0到n-1 ,并且是等概率的。
n+1是划分过程的时间,右边是递归产生的平均时间
在求和中的T(k)和T(n-k-1)是相等的,因为k=0到n-1的时候,k和n-k-1的范围都是0到n-1 ,因此
可以看到,快速排序在平均情况下时间复杂度仅为O(1.39nlogn)。
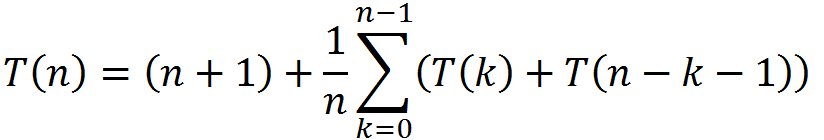
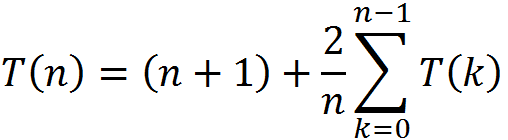

 支付宝打赏
支付宝打赏  微信打赏
微信打赏