雅乐网

基于比较的排序的时间复杂度下界是O(nlogn)，但是当要排序的元素具有一些特殊性质的时候，可以使用非比较的方法突破这种限制。

计数排序

当待排序的元素a[]都是位于区间[0,k]中的整数时，可以使用计数排序。计数排序顾名思义就是统计元素的个数，这需要额外O(k)的空间，我们使用数组c来记录。

首先通过遍历待排序的数组，统计每个元素个数。这时c[i]记录了数组a中i元素的个数。

然后遍历一次统计结果数组，通过c[i] += c[i-1]的操作使c[i]记录a中小于等于i的元素的个数。这样可以直接得到元素在排序好的数组中的下标，例如：数组a中小于等于7的元素有23个，那么排序号的数组中7的下标就是23。

当a中有重复元素的时候，区间  (  c[i] ，c[i+1]  ]就确定了元素i+1的位置。为了保持排序的稳定性，在最终遍历a确定位置的时候要从n开始递减，然后c[i]递减，这样可以保证后面的元素排序好后还是位于后面。

计数排序的时间复杂度为O(n)，但排序不是原址的，空间复杂度为O(max(k, n))。

//计数排序
void countingSort(int a[], int n)
{
	int *b = new int[n];	//存放结果
	int max = 0;
	int i;
	for (i = 0; i < n; ++i)
	{
		if (a[i] > max)
			max = a[i];
	}
	int *c = new int[max+1];	//c[i]记录数组a中比i小的数字有多少个
	for (i = 0; i < max+1; ++i)
		c[i] = 0;

	for (i = 0; i < n; ++i)
		++c[a[i]];
	for (i = 1; i < max+1; ++i)
	{
		c[i] += c[i-1];
	}

	for (i = n-1; i >= 0; --i)
	{
		b[--c[a[i]]] = a[i];

	}

	for (i = 0; i < n; ++i)
	{
		a[i] = b[i];
	}

	delete[] b;
	delete[] c;
}

基数排序

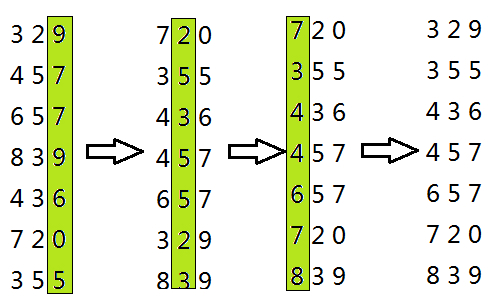
基数排序通过分别按某一位进行排序，先从最低位开始排序，再从次低位，最后到高位。排序时，元素的权值是元素的某一位，而且要使用稳定的排序算法来进行排序。

10进制数字的某一位范围是0-9 ，这非常适合使用计数排序。

#include <cstdio>
#include <cstdlib>
#include <ctime>
#include <cmath>


//返回整数a的低第th位
int nth(int a, int th)
{
	int k = 1;
	for (int i = 1; i < th; ++i)
		k *= 10;
	return (a / k) % 10;
}
//按照低第th位进行排序
//k进制数 
void sortByRank(int a[], int n, int k, int th)
{
	int *b = new int[n];	//存放结果
	int max = k;
	int i;
	int *c = new int[max];	//c[i]记录数组a中比i小的数字有多少个
	for (i = 0; i < max; ++i)
		c[i] = 0;

	for (i = 0; i < n; ++i)
		++c[nth(a[i], th)];
	for (i = 1; i < max; ++i)
	{
		c[i] += c[i-1];
	}

	for (i = n-1; i >= 0; --i)
	{
		b[--c[nth(a[i], th)]] = a[i];

	}

	for (i = 0; i < n; ++i)
	{
		a[i] = b[i];
	}

	delete[] b;
	delete[] c;
}

//k进制正整数 基数排序
void radixSort(int a[], int n, int k = 10)
{
	int max = 0;
	int i;
	for (i = 0; i < n; ++i)
	{
		if (a[i] > max)
			max = a[i];
	}
	int p = 0;
	if (max != 0)
	{
		while ((max = (max / 10)))
			++p;
		++p;
	}

	for (i = 1; i <= p; ++i)
	{
		sortByRank(a, n, k, i);
	}
}


int main()
{
	const int N = 109;
	int a[N] ;
	int i;
	srand((int)time(0));	//生成随机数组
	for (i = 0; i < N; i++)
		a[i] = rand() % N;


	for (i = 0; i < N; ++i)
		printf("%d ", a[i]);

	radixSort(a, N);
	putchar('\n');
	putchar('\n');

	for (i = 0; i < N; ++i)
		printf("%d ", a[i]);
	
	return 0;
}

基数排序的时间复杂度也为O(n)。