给定K个整数组成的序列{ N1, N2, …, NK }，“连续子列”被定义为{ Ni, Ni+1, …, Nj }，其中 1 <= i <= j <= K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 }，其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序，计算给定整数序列的最大子列和。
遍历算法 O(n^3)的算法
这种方法遍历所有的序列和。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
int maxSubseqSum1(int a[], int n) { int i, j, k; int sum = 0; int max_sum = 0; for (i = 0; i < n; ++i) { for (j = i; j < n; ++j) { //计算i到j的和 sum = 0; for (k = i; k <= j; ++k) { sum += a[k]; } if (sum > max_sum) max_sum = sum; } } return max_sum; } |
遍历算法 O(n^2)的算法
上面的算法中，一个子列加上一个元素，并没有直接利用之前子列的和，而是重新计算。可以利用子列的和加上新来的元素，算法的复杂度为O(n^2)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
int maxSubseqSum2(int a[], int n) { int i, j; int sum = 0; int max_sum = 0; for (i = 0; i < n; ++i) { sum = 0; for (j = i; j < n; ++j) { sum += a[j]; if (sum > max_sum) max_sum = sum; } } return max_sum; } |
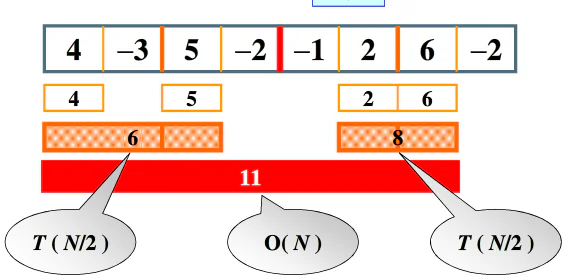
分而治之的O(nlogn)的算法
找最大子列，可能在左半边，也可能在右半边，也可能跨越了中间。
代码如下：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
#include <cstdio> int max(int a, int b, int c) { if (a > b && a > c) return a; else if (b > a && b > c) return b; else return c; } int maxSubArray(int a[], int lo, int hi); int maxSubArray_mid(int a[], int lo, int hi, int mi); int main() { int a[10] = {2, -7, 4, -6, 5, 8, -1, -7, 4, 6}; printf("%d\n", maxSubArray(a, 0, 9)); return 0; } //最大子列和 范围是a[lo]到a[hi] int maxSubArray(int a[], int lo, int hi) { if (lo == hi) return a[lo]; //递归基：当只有一个元素时，最大子列和是该元素自己 int mi = (lo + hi) / 2; int l = maxSubArray(a, lo, mi); //左半部分最大子列和 int r = maxSubArray(a, mi+1, hi);//右半部分最大子列和 int m = maxSubArray_mid(a, lo, hi, mi); //跨越中间的最大子列和 return max(l, r, m); } int maxSubArray_mid(int a[], int lo, int hi, int mi) { int maxl = 0; int maxr = 0; int i; //向左找最大和 int sum = 0; for (i = mi - 1; i >= lo; --i) { sum += a[i]; if (sum > maxl) maxl = sum; } //向右找最大子列和 sum = 0; for (i = mi + 1; i <= hi; ++i) { sum += a[i]; if (sum > maxr) maxr = sum; } return a[mi] + maxl + maxr; } |
时间复杂度 T(n) = 2T(n/2) + n ，由主定理可知，时间复杂度为O(nlogn)
复杂度O(n)的算法
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
int maxSubseqSum4(int a[], int n) { int i; int sum = 0; int max = 0; for (i = 0; i < n; ++i) { sum += a[i]; if (sum > max) //如果和大于最大值 就更新最大值 max = sum; if (sum < 0) //如果和是负数 就舍弃 sum = 0; //因为负数加上后面的序列和只会让和变小 } return max; } |
支付宝打赏 
微信打赏